Fuerza Centrípeta y Conservación de la Energía (Fis 151/Fis 1513)
From Uv
Contents |
Fuerza Centrípeta y Conservación de la Energía
Objetivo
Predecir y calcular los parámetros necesarios para que el carro de una vuelta en el loop sin caerse.
Introducción
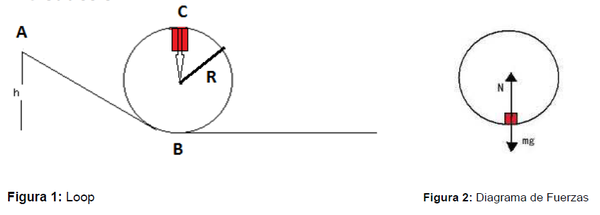
Por conservación de la energía y despreciando el roce se tiene
Aplicando la ecuación de Newton, en el punto C de la figura 1:
como,
y usando que: y
:
ocurre cuando
, en este caso:
Materiales
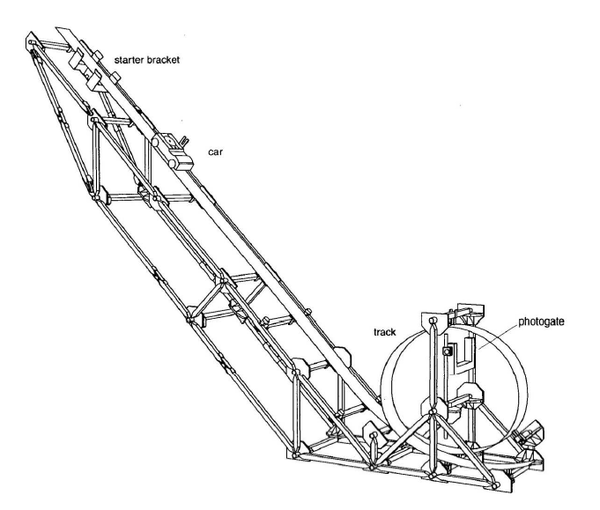
- Sistema Reticulado Pasco “Montaña Rusa”
- Fotocelda
- Barras
- 2 vigas #1
- 2 vigas #2
- 13 vigas #3
- 28 vigas #4
- 14 vigas #5
- 25 conectores medio giro
- 3 conectores XYZ
- 1 conector plano
- 4 conectores para deslizamiento
- 10 conectores angulares
- 6 conectores rectos
- 1 soporte de partida (riel)
- 1 varilla mediana
- 1 riel
- Sujeta pistas tipo clips
- PC con Programa Data Studio
Construcción del Loop
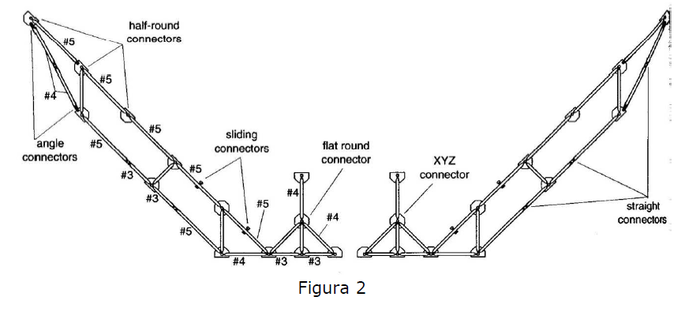
- 1.- Arme ambos lados del loop como indica la Figura 2:
- 2.- Use 14 vigas #4 para conectar ambos lados del loop.
- 3.- Una vez armada la estructura, conecte 13 clips (sujeta pista).
- 4.- Ajuste el riel de la forma más circular posible.
- 5.- Conecte la fotocelda , así como indica la figura 5.
- 6.- Una vez armada la estructura, atorníllele al carro una masa (disco circular).
- 7.- Ubique el carro en el riel y suéltelo. Deberá llegar hasta el final de la pista. Realice los ajustes necesarios para que el carro realice una vuelta circular y llegando hasta el final de la pista.
Montaje del Sensor
- i) Deberá usar la fotocelda para medir la velocidad del carro.
- ii) En el menú de configuración conecte el sensor en la entrada digital.
- iii) Seleccione fotocelda y regleta . La constante de la fotocelda es de
.
Procedimiento
Parte I: Análisis Cualitativo
- 1.- Mida la altura del Soporte de partida, el radio del loop y cualquier otra magnitud que Ud. considere importante.
- 2.- Prediga la máxima velocidad que debe tener el carro para que este de la vuelta al loop.
- 3.- Aplique la ecuación de Newton (o movimiento) en el punto de mayor altura del loop.
- a) ¿Cuáles son las fuerzas que actúan sobre el carro?
- b) ¿Cuál es la aceleración del carro en el punto de mayor altura, si este da la vuelta al loop?
- c) ¿Cuál es el valor de la Normal que el loop ejerce sobre el carro, cuando este tiene la mínima velocidad que le permite dar la vuelta?
- d) Calcule la velocidad mínima para que el carro de la vuelta al loop.
- 4.- Prediga el punto mínimo sobre el riel o la mínima altura desde la cual se podrá soltar el carro y le permita dar una vuelta completa. Discuta su razonamiento.
Parte II: Usando data Studio
- 1.- Sin registrar datos aún, suelte el carro posicionándolo en diferentes puntos sobre el riel. Asegúrese de que un compañero atrape el carro al final del riel. Encuentre el punto más bajo del cual Ud. puede soltar el carro y que gire alrededor del loop. Marque este punto y mida su altura con respecto al piso.
- 2.- Inicie el registro de datos (START)
- 3.- Ubique el carro en el soporte de partida que está sobre el riel y suéltelo.
- 4.- Con el registro de datos aún funcionando, ubique el carro sobre el riel pero esta vez en otra posición (bajo el soporte de partida) y suéltelo nuevamente.
- 5.- Repita este proceso varias veces, pero cada vez bajando mas sobre el riel, hasta llegar al punto que Ud. marcó (1.-)
- 6.- Presione STOP
Análisis
- A partir del registro de datos, determine la velocidad del carro en la parte superior del loop, cada vez que de una vuelta. Repita unas cinco veces. Registre cada valor. Obtenga el valor medio de la velocidad en este punto.
- ¿Cuál es la velocidad mayor registrada?. Compárela con la estimación realizada en la Parte I (punto 2)
- ¿Cuál es la velocidad mínima registrada?. Compárela con la estimación realizada en la Parte I (punto 3d)
- ¿Cuál es la altura más baja, desde la cual Ud. puede soltar el carro?. Compárela con la estimación realizada en la Parte I (punto 4)