Conservación de la Energía (Fiz010 DS)

Conservación de la Energía

Objetivo

Estudiar empíricamente la conservación de la Energía Mecánica realizando experimentos de conversión de Energía Potencial de un resorte en Energía Cinética de masas en movimiento.

Equipamiento

- Carros Dinámicos

- Riel

- Fotocelda

- Regleta

- Balanza

- Computador PC con interfaz PASCO

- Programa DATA STUDIO

Teoría

La Energía Potencial de un resorte comprimido una distancia respecto de la posición de equilibrio está dada por la relación

donde es la constante elástica del resorte. De acuerdo con la Ley de Hooke, la fuerza que ejerce el resorte es directamente proporcional a la distancia que el resorte es comprimido o estirado, es decir,

donde es la constante de proporcionalidad. Esta relación permite determinar la constante de proporcionalidad experimentalmente, aplicando diferentes fuerzas al resorte para estirarlo diferentes distancias. Al graficar la fuerza vs. la distancia, se obtiene la constante como la pendiente del gráfico. Si la energía mecánica se conserva, al liberar el resorte comprimido, la Energía Potencial acumulada se transformará en energía Cinética, estando ésta dada por la relación,

donde es la masa unida al resorte y la velocidad.

Montaje Experimental

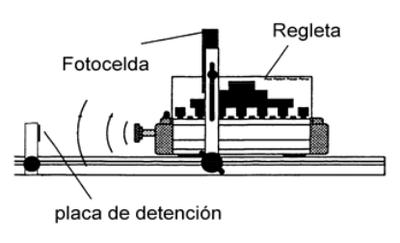
Monte el riel, la polea y la fotocelda de acuerdo con lo indicado en la figura 1. Ajuste los tornillos de nivel del riel de modo que el carro ubicado sobre éste permanezca en reposo, sin moverse hacia ninguno de los extremos. Coloque la regleta en la parte superior de un carro, como muestra la figura.

Figura 1: Montaje experimental.

Primera parte: Determinación de la constante del resorte

Procedimiento Experimental

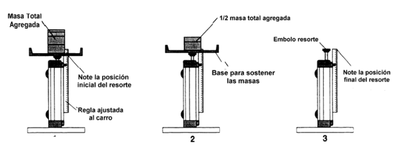
1) Posicione el carro dinámico sobre uno de sus extremos, de tal forma que el resorte del carro quede apuntando hacia arriba, así como lo indica la figura 2. Fije una regla al carro y ajústela de tal modo que la línea del cero coincida con la línea superior del resorte (en posición no comprimida).

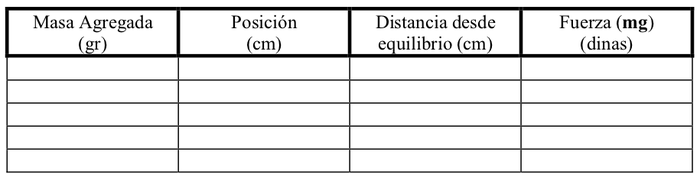
2) Cuidadosamente agregue suficientes masas en la parte superior del resorte de tal forma que quede muy comprimido. Registre esta masa y la compresión correspondiente (posición inicial) del resorte en la tabla 1.

3) Quite aproximadamente un cuarto de la masa usada en el punto (2) valores de la nueva masa y de en la tabla 1.

4) Repita el punto (3) y registre los hasta que no quede mas masa sobre el resorte.

5) Realice un gráfico v/s usando sus datos y determine la pendiente de la mejor línea trazada a través de los puntos.

Figura 2: Calibración del carro.

Tabla 1 Datos para determinar la constante elástica

Tabla 1

Segunda Parte: Energía Cinética

5) Remueva la cuerda del carro y comprima al máximo el resorte, de modo que éste quede fijo en la posición comprimida. Ubique el carro sobre el riel, con el extremo del resorte en contacto con la placa de detención. Mida la distancia en que se ha comprimido el resorte y anote el resultado en la Tabla 2.

6) Posicione la fotocelda de modo que la regleta sobre el carro empiece a pasar a través de la fotocelda justo en el momento en que el extremo de resorte en posición no comprimida deja de estar en contacto con la placa de detención. (Note que esta situación corresponde a la de máxima velocidad del carro). Ajuste la altura de la fotocelda de modo que ésta sea bloqueada por las barra de de la regleta.

7) En el programa DATA STUDIO presione el icono del conector digital y conéctelo en el canal 1 seleccionando Photogate (Fotocelda). En el ícono de la regleta seleccione el valor de la constante de la banda a utilizar .Deslice el carro frente a la fotocelda para constatar su correcto funcionamiento. Asegúrese que la fotocelda está correctamente alineada con la fila de de la regleta y ésta interrumpe adecuadamente el haz de luz.

NOTA: Asegúrese que en el ícono de la regleta esté activado la medición de velocidad.

8) Cuando esté listo para iniciar la recolección de datos presione el botón START (Inicio). La medición empezará cuando el haz de iluminación de la fotocelda sea bloqueado por primera vez por las barras de la regleta. Suelte el mecanismo de fijación del resorte comprimido introduciendo en la apertura correspondiente un lápiz u otro objeto similar. Luego que la regleta sobre el carro ha pasado frente a la fotocelda, presione el botón STOP (Detener) para detener el proceso de medición. Luego seleccione la opción Table (Tabla) del menú Display (Pantallas)

9) Siga el procedimiento de análisis de los experimentos anteriores para graficar los

datos y calcular la velocidad del carro.

10) Repita la operación anterior cinco veces, anotando los resultados en la Tabla2. Agregue una barra de masa al carro y repita las mediciones anteriores.

Distancia que se comprime el resorte: _____________________

Tabla 2 Medición de Velocidades

Tabla 2

Análisis de Datos

a) Usando los datos de la Tabla 1, grafique en papel milimetrado la fuerza (mg) aplicada al resorte vs. la distancia comprimida. Dibuje la mejor línea recta que pase por los puntos del gráfico y determine su pendiente. La pendiente de esta recta es igual a la constante elástica efectiva, , del resorte. Anote su resultado.

=_________________________

b) Calcule la Energía Potencial del resorte comprimido en la segunda parte del experimento.

c) Usando las velocidades promedio, calcule la Energía Cinética para los casos del carro con y sin masa adicional, anotando sus resultados en la Tabla 3.

d) Calcule la diferencia porcentual entre la Energía Potencial del resorte y la Energía Cinética. Anote su resultado en la Tabla 3.

Tabla 3 Resultados

Tabla 3

Preguntas

1. ¿Cuál de las energías medidas resulta ser mayor: la Cinética o la Potencial?. Justifique.
2. ¿Cómo es la energía final con respecto a la inicial?.
3. ¿En que se ha transformado la diferencia de energía del sistema?.Discuta su resultado.
4. Al agregar masa adicional al carro, ¿Por qué no cambia la Energía Potencial del resorte?
5. Para una idéntica compresión inicial del resorte, ¿Cómo se comparan las Energías
6. Cinéticas resultantes para el carro solo y el carro con masa adicional? Discuta su resultado.
7. ¿Qué significado físico tiene la constante elastica del resorte obtenida por Ud.?. Indique sus unidades.
8. ¿Qué representa el área bajo la curva del grafico vs  ?. Explique.
9. Interprete físicamente el signo menos de la ecuación que representa la ley de Hooke.