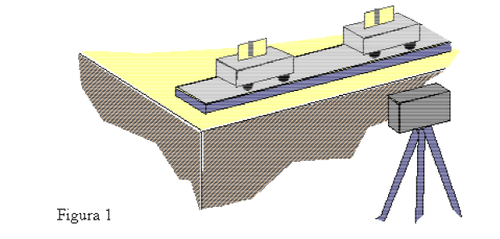
Dinámica de Colisiones en 1-D (Fiz 121)

Dinámica de Colisiones en 1-D

Objetivo

Estudiar la dinámica de colisiones en movimiento unidimensional.

Materiales

- Cámara VideoCom

- Computador con programa VideoCom Movimiento

- Riel Pasco

- Carros dinámicos Pasco.

- Balanza

- Programa para procesamiento de datos.

Introducción

Las variables dinámicas que permiten describir cuantitativamente un proceso de colisión entre dos objetos son el momentum lineal y la energía mecánica. El momentum lineal está dado por la expresión

$LaTeX: \vec{p}=m\vec{v}$

donde $LaTeX: m$ es la masa del objeto en movimiento y $LaTeX: \vec{v}$ su velocidad. La energía mecánica está dada por la expresión,

$LaTeX: E = K +U$

donde K es la energía cinética y U la energía potencial. El término de energía cinética está dado por la expresión,

$LaTeX: K=\frac{1}{2}mv^2$

y el término de energía potencia incluye energía potencial gravitatoria, además de otros términos, tales como energía potencial asociada a deformación elástica.

En este laboratorio se estudiará la evolución de estas variables dinámicas en procesos de colisión unidimensional entre dos cuerpos. El experimento se hará sobre una superficie nivelada horizontalmente, por lo que en este caso el término de energía potencia gravitatoria es constante.

Los cuerpos a colisionar incluyen resortes, que al comprimirse acumulan energía potencial elástica. En este caso, el término de energía potencial está dado por la expresión,

$LaTeX: U=\frac{1}{2}k (\Delta x)^2$

donde $LaTeX: \Delta x$ es la compresión del resorte y $LaTeX: k$ una constante específica al resorte. De este modo, la expresión para la energía mecánica asociada a una de las masas en movimiento es

$LaTeX: E=\frac{1}{2}mv^2+\frac{1}{2}k(\Delta x)^2$

El cambio en la energía cinética del objeto está relacionado con el trabajo realizado sobre éste. Así,

$LaTeX: W = \Delta K$

donde $LaTeX: W$ es el trabajo realizado sobre el objeto. El trabajo está dado por la integral de la fuerza sobre el objeto, a lo largo de la trayectoria, mediante la expresión,

$LaTeX: W_{ab}=\int_{x_a}^{x_b}\vec{F} \cdot d \vec{x}$

A su vez la fuerza se relaciona con la aceleración que experimenta el objeto a través de la 2a Ley de Newton

$LaTeX: \vec{F} = m\vec{a}$

A partir de las expresiones anteriores, considerando un movimiento unidimensional, se puede relacionar la aceleración con la energía cinética mediante la ecuación

$LaTeX: \int madx = \frac{1}{2} mv^2$

Montaje Experimental

Figura 1: Montaje del del experimento.

Procedimiento

En este laboratorio debe realizar al menos los siguientes experimentos:

1. Colisión entre dos carros por choque frontal, con alternativas de un carro en movimiento y el otro detenido y ambos en movimiento.

2. Colisión entre dos carros por choque mediante un resorte, con alternativas de un carro en movimiento y el otro detenido y ambos en movimiento. En este caso el análisis de los resultados requiere conocer la constante elástica del resorte que participa en la colisión.

3. Colisión plástica entre dos carros, con alternativas de un carro en movimiento y el otro detenido y ambos en movimiento.

Para el procesamiento cuantitativo de sus datos experimentales necesario conocer la masa de los objetos que colisionan.

Para cada uno de los experimentos siga el siguiente procedimiento general:

• Registre el movimiento de los carros.

• Genere los gráficos $LaTeX: x_1$ versus $LaTeX: t$, y $LaTeX: x_2$ versus $LaTeX: t$, donde $LaTeX: x_1$ y $LaTeX: x_2$ representan la posición de los carros.

• A partir de los datos de $LaTeX: velocidad$ versus $LaTeX: tiempo$, genere gráficos para $LaTeX: p_1$ versus $LaTeX: t$, $LaTeX: p_2$ versus $LaTeX: t$ y $LaTeX: (p_1 +p_2)$ versus $LaTeX: t$.

• A partir de los datos de $LaTeX: velocidad$ versus $LaTeX: tiempo$, genere gráficos para $LaTeX: K_1$ versus $LaTeX: t$, $LaTeX: K_2$ versus $LaTeX: t$ y $LaTeX: (K_1 +K_2)$ versus $LaTeX: t$.

• A partir de los datos de aceleración vs. tiempo, genere gráficos para W1 vs. t y W2 vs. t. Note que en este caso deberá realizar una integración sobre gráficos aceleración vs. posición.

• Compare los gráficos de energía cinética versus tiempo y trabajo versus tiempo.

• En el caso de los choques con resorte, usando sus datos de posición y tiempo y el valor medido para la constante elástica, genere un gráfico para la evolución temporal de la energía potencial acumulada en el resorte. Obtenidos los datos para la evolución temporal de la energía potencial, genere un gráfico energía mecánica versus tiempo.

Usando la información contenida en los distintos gráficos generados a partir de los datos experimentales, discuta la evolución temporal del momentum lineal y la energía mecánica en una situación de colisiones en una dimensión.