Colisiones: Conservación de momento y energía cinética (Fiz0112)
Contents |
Colisiones: Conservación de momento y energía cinética
Objetivos
- Verificar experimentalmente la ley de conservación del momento lineal en colisiones elásticas e inelásticas.
- Estudiar, para cada tipo de colisión, la conservación de la energía cinética.
Introducción
El momento lineal de una partícula se define como el producto de su masa por la velocidad, . La segunda ley de Newton puede escribirse en términos del momento como: la variación en el tiempo del momento lineal de una partícula es igual a la fuerza neta que actúa sobre la misma,
Si la partícula se encuentra aislada, esto es si , entonces el momento lineal se conserva, i.e.
.
Para un sistema de N partículas, el momento lineal del sistema se define como la suma vectorial de los momentos de cada una de las partículas,
De acuerdo con la Tercera Ley de Newton para cada par de partículas las fuerzas de interacción se cancelan y la ecuación (1) se escribe como:
entonces, si el sistema de partículas está aislado, esto es, si sobre éste no actúan fuerzas externas el momento lineal del sistema se conserva:
En una colisión entre partículas para un sistema aislado, como hemos visto el momento lineal es el mismo antes y después de la colisión. En cambio, para la energía cinética no podemos afirmar lo mismo. En relación a este hecho clasificamos las colisiones en: Elásticas e Inelásticas.
Una colisión elástica entre dos objetos es aquella en la que la energía cinética se conserva, en cambio, por una colisión inelástica entendemos aquella en la que la energía cinética del sistema antes y después de la colisión no es la misma. Las colisiones después de las cuales los objetos permanecen unidos, se denominan perfectamente inelásticas.
En este laboratorio estudiaremos la ley de conservación del momento lineal de un sistema de dos partículas a través de experimentos simples de colisiones elásticas y perfectamente inelásticas.
Experimento 1: Colisión perfectamente inelástica
En este experimento verificaremos la Ley de Conservación del Momento Lineal para un sistema de dos cuerpos que efectúan una colisión perfectamente inelástica.
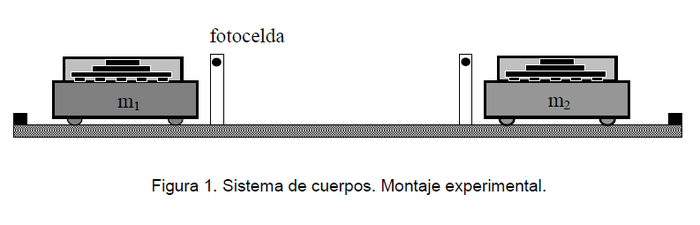
Tenemos dos carros dinámicos que pueden desplazarse a lo largo de un riel horizontal (ver Figura 1). Inicialmente el carro 1 se mueve con velocidad acercándose al carro 2 que se encuentra en reposo (
). Luego de la colisión los dos permanecen unidos. De la conservación del momento lineal del sistema (Eq. 4) sabemos que:
donde es la velocidad de los dos carros unidos luego de la colisión.
Equipamiento
- Carros dinámicos.
- Riel.
- Balanza.
- Fotoceldas.
- Computador con interfaz Science Workshop Pasco.
- 2 Bloques de (aprox.)
Montaje experimental y procedimiento
- * Monte el sistema de los dos carros con las regletas con barras acopladas a los mismos de acuerdo a lo indicado en la Figura 1. Posicione las fotoceldas de modo tal que la colisión ocurra entre ellas. Ajuste las fotoceldas de modo que los haces sean bloqueados por la barra de
de la regleta y conéctelas en los canales de la interfaz. Seleccione para cada canal Photogate. Haga doble clic en el icono de las fotoceldas e ingrese
que corresponde a los
- * Para comenzar a medir presione Start, y Stop para detener la adquisición de datos. Una vez tomados los datos, del menú Display seleccione Table, para poder obtener así los datos recolectados.
- * Disponga los carros con los discos de velcro de manera tal que permanezcan unidos luego de la colisión.
- * Para las mediciones ubique el carro de masa
entre las fotoceldas e imparta cierta velocidad al carro de masa
.
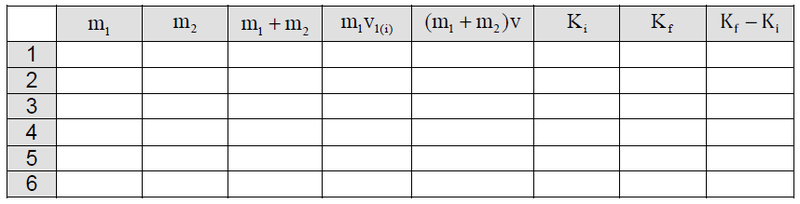
- * Usando los dos bloques para variar la masa de los carros, efectúe diferentes mediciones de la velocidad inicial y final. Por ejemplo, puede empezar por colocar los dos bloques sobre el carro 1. (Observe que en total serán 6 las mediciones posibles.) Con los datos recolectados monte la siguiente tabla donde
y
representan las energías cinéticas antes y después de la colisión respectivamente.
- * Haga un gráfico de
versus
y verifique si el momento lineal del sistema se conserva en la colisión. Analice sus resultados.
- * Demuestre (en el Acta) que el valor teórico de la pérdida de energía cinética en la colisión es,
- Sus resultados experimentales, ¿están de acuerdo con esto? Analice y comente.
Experimento 2: Colisión elástica
En este experimento verificaremos la conservación tanto del momento lineal como de la energía cinética para un sistema de dos cuerpos que colisionan elásticamente.
En un sistema similar al del experimento anterior, el carro 1 se mueve con velocidad al encuentro del carro 2 que se está en reposo (
). Luego de la colisión las velocidades de ambos carros son
y
.
Dado que en este tipo de colisión se conservan momento y energía, podemos obtener las velocidades finales en términos de la velocidad inicial :
Montaje experimental y procedimiento
El montaje experimental para este experimento es básicamente el mismo que el del anterior.
- * Oriente los carros de manera tal que podamos simular una colisión elástica.
- * Ubique el carro de masa
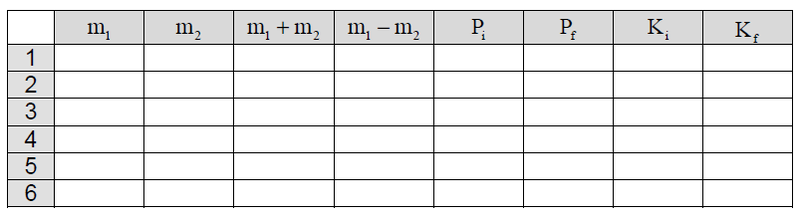
- * Usando los dos bloques para variar la masa de los carros, efectúe diferentes mediciones de la velocidad inicial y final. Por ejemplo, puede empezar por colocar los dos bloques sobre el carro 1. (Observe que en total serán 6 las mediciones posibles.) Con los datos recolectados monte la siguiente tabla donde
- * Realice un gráfico de
versus
y verifique si el momento lineal del sistema se conserva en la colisión.
- * ¿Qué sucede si
?. Si es necesario extrapole el gráfico.
- * Realice ahora un gráfico
versus
y verifique si la energía cinética en la colisión elástica se conserva.
- * Analice y comente sus resultados.
Partes Adicionales
Usando materiales asociados a los montajes previos, y algunos recursos extra disponibles en el laboratorio, usted podría estudiar:
- 1. Conservacion de momentum de un carro cuya masa varia mientras se mueve
- 2. Conservación de momentum en el choque de más de dos carros
- 3. Teorema trabajo-energía, haciendo chocar un carro contra una masa que se desplace una cierta distancia. Midiendo esa distancia y el cambio de momentum del carro que choca, puede determinar el coeficiente de roce.
En esta sección, usted debe elegir al menos uno de estos fenómenos para estudiar. Debe registrar en su Acta lo que está analizando, cómo lo hace, los inconvenientes y resultados obtenidos, análisis, etc. Si usted se le ocurre algo interesante de medir, dentro del contexto del curso, puede agregarlo a la lista de “Adicionales”
