Distancia Focal de una Lente Delgada (Fis 1520)

Distancia Focal de una Lente Delgada

Objetivo

Análisis de diversas lentes delgadas.

Equipamiento

− Banco Optico

− Lente convexa

− Lente concava

− Fuente de luz (Ampolleta)

− Fuente de poder para la ampolleta

− Pantalla

− Regla

− Huincha de medir

Teoría

Para una lente delgada se cunple la Ley de Gauss

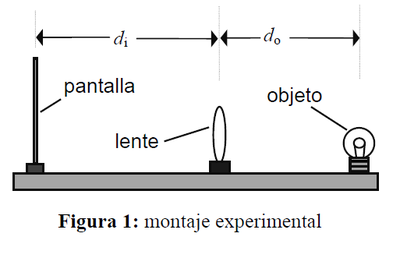
donde es la distancia focal, do es la distancia entre el objeto y la lente, y di es la distancia entre la imagen y la lente. Ver figura 1.

Procedimiento

I. Distancia Focal Usando un Objeto en el Infinito

1) Usando la lente convexa, enfoque una luz distante sobre una hoja de papel.

2) Mida la distancia desde la lente al papel. Esta es la distancia de la imágen.

3) En la fórmula para la lente delgada, tome el límite en que la distancia de objeto va al infinito.

Obtenga la distancia focal: = ____________

II. Distancia Focal Graficando versus

1) En un banco óptico posicione una lente convexa y a ambos extremos una ampolleta y una pantalla. Posicione la lente entre el objeto y la pantalla.

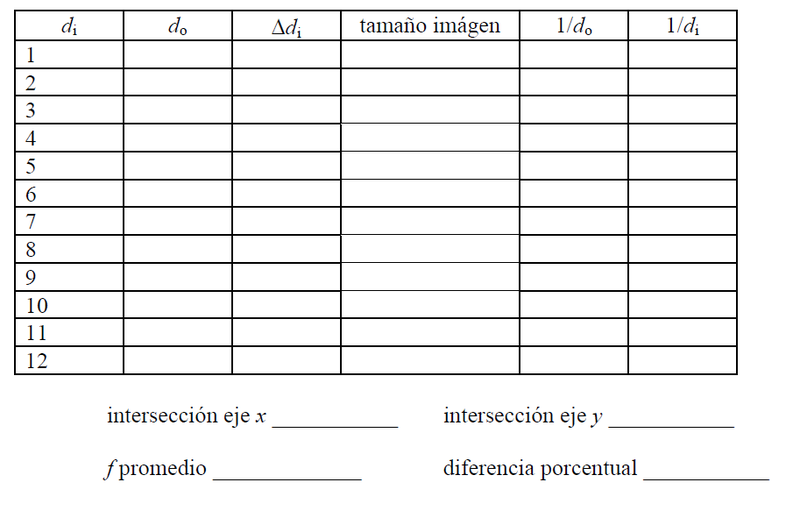
2) Mueva la lente a una posición en que se forme una imagen del objeto sobre la pantalla. Mida la distancia imagen y la distancia do objeto. Moviendo la pantalla en torno a la posición correspondiente a , haga una estimación del rango de distancia en que la imagen puede ser considerada en foco. Considere este rango como su error en la determinación de la posición de la imagen. Anote todas sus mediciones en la Tabla 1.

3) Mida el tamaño de la imagen y el objeto, para esta posición.

4) Dejando la pantalla en la posición di anterior, mueva la lente a una segunda posición donde la imagen esté en foco (no mueva la pantalla o la fuente de luz). Mida la distancia imagen y la distancia objeto, y determine nuevamente el rango de incerteza correspondiente en la distancia imagen.

5) Mida también el tamaño de la imagen para esta posición.

6) Mueva la pantalla hacia el objeto, repitiendo el punto (2) hasta que sea posible encontrar una sola posición de la lente en que la imagen esté enfocada. Esto le dará seis conjuntos de datos (en total doce pares de puntos ), los cuales deberá escribirlos en la tabla 1.

7) Grafique versus. , usando los doce puntos. Grafique los rangos de incerteza en los valores . De acuerdo con la Ec. (1), el gráfico debería resultar en una línea recta, en que la intersección con los ejes x e y es igual a .

8) Encuentre la diferencia porcentual entre los dos valores de la distancia focal correspondientes a ambas intersecciones. Tome el promedio de los dos valores y encuentre la diferencia porcentual entre el valor así obtenido y la distancia focal encontrada en la Parte I. Discuta el efecto de la precisión en la medición de , debido a la incerteza en las mediciones de .

9) Usando solamente los dos primeros conjuntos de datos, use las distancia objeto y distancia imagen, para encontrar la magnificación en cada posición de la lente.

Preguntas

a) La imagen que forma la lente es, ¿Derecha o invertida? Discuta su resultado experimental.

b) Explique por qué, para una distancia objeto - pantalla dada, hay dos posiciones en las que la imagen se encuentra en foco.

III. Magnificación de una Lente Convergente

Toda lente convergente o divergente amplifica o minimiza las imágenes cuya relación viene dada por:

Otro método para determinar la magnificación es a partir de la medición del tamaño del objeto e imagen es :

1) Use las ecuaciones (2) y (3) para encontrar la magnificación. Para ello utilice las dos primeras filas de datos de la tabla 1. Compare los resultados obtenidos en ambos casos.

2) Encuentre las diferencias porcentuales de la Magnificación obtenidos por la ecuaciones (2) y (3).

Preguntas

a) ¿Puede determinar alguna dependencia empírica entre la incerteza asociada al tamaño de la imagen y el valor de correspondiente a distintas posiciones del objeto? Discuta.

b) ¿ Cuál de los dos métodos considera Ud. que es el más exacto para obtener ?. Justifique.

IV. Análisis para la Distancia Focal de una Lente Divergente

El procedimiento de la parte II que ha empleado no puede utilizarse si la lente es divergente, ya que esta por si sola no puede formar una imagen real. Sin embargo la distancia focal de una lente divergente puede calcularse si ella conforma con otra lente convergente un sistema que sea convergente.

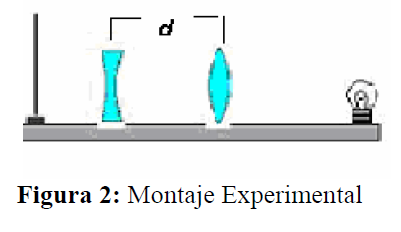
1) Como procedimiento para calcular la distancia focal del lente divergente, se sugiere el siguiente montaje:

En el cual se inserta primero la lente convergente entre el objeto y la pantalla, cuya posición es tal que se vea una imagen enfocada. Luego se inserta la lente divergente entre la pantalla y la lente convergente. En este instante proceda a medir las distancias respecto a la divergente, o sea la distancia entre la imagen proyectada en la pantalla y la lente divergente es (negativa). ¿Porqué?

2) Proceda a mover la pantalla hasta observar la imagen nítida. Mida la distancia imagen entre la lente divergente y la pantalla ()

3) Aplique la Ley de Gauss para obtener la distancia focal del lente divergente.

Preguntas

a) ¿Cuánto vale la distancia focal de la lente ?, ¿Cuál es el error de su medida?.

b) ¿Por qué se debe usar una lente convergente para obtener la distancia focal del lente divergente?

c) Realice un diagrama de Rayos que explique el experimento anterior.

V. Sistema de Lentes

Se trabajará con el mismo montaje anterior, un sistema de lentes convergente y divergente, y con la adquisición de datos del punto 2) del análisis anterior, procediendo a medir la distancia d entre las lentes.

La formula que representa el sistema de lentes es:

donde es la distancia focal equivalente del sistema, y son las respectivas distancias focales de las dos lentes que conforman el sistema y d es la separación entre ellas. Calcule para la distancia d que Ud. eligió en (1) de la parte IV, la distancia focal equivalente de su sistema.

Preguntas

a)¿Cómo clasificaría éste sistema de lentes, convergente o divergente?.

Tabla 1