Análisis Espectral: Determinación de la Constante de Rydberg (Fiz0311)

1 Análisis Espectral: Determinación de la Constante de Rydberg
2 Parte I: Determinación de la constante de la red de difracción utilizando las líneas del espectro de Mercurio
3 Parte II: Determinación de la Constante de Rydberg utilizando el espectro visible del Hidrógeno.
4 Apéndice 1: Las Longitudes de Onda
5 Apéndice 2: Los Tubos de Descarga
6 Apéndice 3: Vernier

Análisis Espectral: Determinación de la Constante de Rydberg

Objetivo

Determinar la constante de Rydberg.

Equipamiento

- Goniómetro

- Red de difracción

- Tubo de descarga espectral de hidrógeno

- Diodo láser

- Lámpara de Mercurio

Introducción

Difracción

Figura 1: Difracción por una red, con incidencia normal.

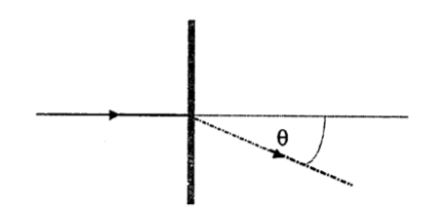
La ecuación para una red de difracción, en una situación en que la luz incide normal sobre la red, está dada por:

$m \lambda = d \cdot \sin(\theta) \qquad\qquad\qquad (1)$

donde, $m$ es Orden del espectro observado, $d$ la constante de separación de la red y $\theta$ el ángulo de difracción medido con respecto a la normal de la red (fig.1).

Emisión

En 1913 Niels Bohr formuló una teoría para explicar el espectro del hidrógeno, basados en las investigaciones de Planck sobre la radiación del cuerpo negro, Bohr comenzó suponiendo que el electrón giraba en órbitas circulares alrededor del núcleo. Luego postuló la existencia de ciertas órbitas estables, en las cuales el electrón puede permanecer sin irradiar. En cada una de ellas, la energía del sistema electrón-nucleo posee un valor característico para ese estado, si por alguna razón el electrón cambia de órbita, el átomo correspondiente absorberá o irradiará una cantidad determinada de energía igual a la diferencia de energía total entre sus estados inicial o final, o sea

$h\nu=E_i-E_f \qquad\qquad\qquad (2)$

Bohr tomando en consideración que la energía sólo podrá radiarse en determinadas frecuencias, que dependen de la naturaleza del átomo, estableció la siguiente relación:

$\frac{1}{\lambda}=\frac{2\pi^2 m_e Z^2e^4}{h^3 c} \left( \frac{1}{n_f^2}-\frac{1}{n_i^2} \right) \qquad\qquad\qquad (3)$

donde,

$m_e$ : masa del electrón

$Z$ : número atómico

$e$ : carga del electrón

$h$ : constante de Planck

$c$ : velocidad de la luz

$n_f$ : número cuántico del estado final

$n_i$ : número cuántico del estado inicial

A finales del siglo pasado Balmer encontró empíricamente una expresión que relacionaba las líneas conocidas del espectro del hidrógeno. Esta expresión fue refundida por Rydberg en la siguiente ecuación:

$\frac{1}{\lambda}=R_H \left( \frac{1}{4}-\frac{1}{n^2} \right) \qquad\qquad\qquad (4)$

$n=3,4,5...$

donde:

$\lambda$ : longitud de onda de la línea espectral

$R_H$ : constante de Rydberg

$n$ : entero que corresponde al número de orden de cada línea espectral en la serie de Balmer (No es lo mismo que el orden del espectro)

Luego, $R_H=\frac{2\pi^2 m_e Z^2e^4}{h^3 c}$ corresponde a la constante de Rydberg.

La ecuación (1) nos permitirá calcular la constante de Rydberg si conocemos la longitud de onda de la línea espectral y su número de orden en la serie de Balmer.

Montaje Experimental

El Goniómetro

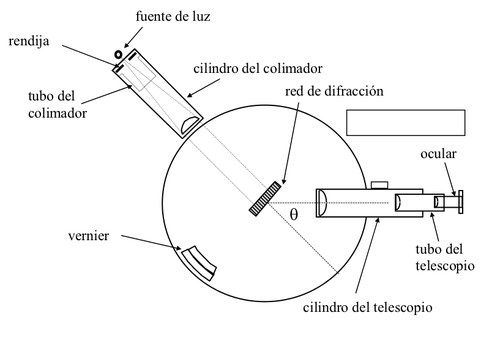
Para la medición de longitudes de onda asociadas a líneas de espectros de emisión se usará un espectrómetro, como el que se muestra esquemáticamente en la figura 2. Este consiste de un colimador con una rendija ajustable de entrada y un telescopio para observación, ambos montados radialmente en torno a una plataforma circular, que posee un vernier para medición de ángulos. Sobre la plataforma se ubica la red de difracción. Existen diversos tornillos de enfoque y fijación, cuyo uso se describe a continuación.

Figura 2: Dibujo esquemático del espectrómetro, con sus partes principales.

Los Tubos de descarga

(See Appendix for more details)

El espectro de radiación que sale de un tubo de descarga de gas contiene todas las frecuencias que se pueden obtener de las transiciones entre dos estados de energía cualesquiera. Así el espectro de radiación emitido por un gas en un tubo de descarga de gas da información directa sobre los niveles de energía de un átomo. Cada elemento tiene sus propias líneas espectrales características.

Parte I: Determinación de la constante de la red de difracción utilizando las líneas del espectro de Mercurio

1) Prepare el goniómetro para realizar óptimas mediciones. Pregúntele al profesor o ayudante.

Figura 3: Goniómetro.

2) Ponga la lámpara de Mercurio en la rendija de entrada y mueva el cilindro del telescopio hasta que la imagen correspondiente al orden cero (imagen sin dispersión) se vea. Mida esta posición cuidadosamente, su valor y su respectivo error.

¿Cuáles son las ventajas y desventajas de tener una rendija de entrada ancha?

3) Mueva el cilindro del telescopio hasta que se vean las líneas espectrales de mercurio. Conviene observar unos cuatro órdenes del espectro (dos con ángulos positivos y dos con ángulos negativos). Identifique la longitud de onda y el orden de cada línea. Mida los ángulos (incluyendo la incerteza debido al error de observación).

4) Utilizando la ecuación 1 realice un gráfico y calcule nuevamente la constante de separación de la red usando las longitudes de onda conocidas del mercurio (ver apéndice 1).

Parte II: Determinación de la Constante de Rydberg utilizando el espectro visible del Hidrógeno.

1) Use un tubo de descarga de hidrógeno como fuente de luz.

2) Mida los ángulos $\theta$ para las principales líneas visibles y calcule las longitudes de onda. Estas líneas son las primeras de la serie de Balmer. Conviene observar tres líneas y unos cuatro órdenes del espectro (dos con ángulos positivos y dos con ángulos negativos).

3) Usando la ecuación 2 y algún método gráfico, calcule (con errores) un valor para la constante de Rydberg.

Apéndice 1: Las Longitudes de Onda

Algunas líneas prominentes del espectro de emisión del Mercurio son $405.5 nm$ (morada), $435.8 nm$ (azul), $546.1 nm$ (verde) y $579.1 nm$ (amarilla).

Apéndice 2: Los Tubos de Descarga

Los átomos de un elemento (hidrógeno, por ejemplo) pueden ser excitados a estados de energía mas altos bombardeándolos con una haz de electrones energéticos. Esto se lleva a cabo en buena forma en un tubo de descarga de gases, que es un tubo cerrado que contiene hidrógeno (o algún otro gas) a muy baja presión y los electrodos en su interior.

El cátodo se calienta para que emita electrones, los cuales son atraídos por el ánodo. Los electrones adquieren así energía móvil al moverse hacia el ánodo y de vez en cuando chocan con un átomo de hidrógeno (u otro gas). En el proceso de choque parte de la energía cinética de los electrones pueden pasar al átomo llevando al electrón (o electrones si es otro gas) del Hidrógeno a un estado de energía mas alta.

Apéndice 3: Vernier

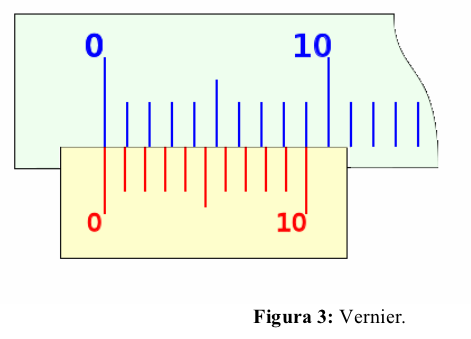
El sistema consiste en una regla sobre la que se han grabado una serie de divisiones según el sistema de unidades empleado, y una corredera o carro móvil, con un fiel o punto de medida, que se mueve a lo largo de la regla.

Si la división cero del nonio coincide con la división cero de la regla, la distancia entre la primera división de la regla y la primera del nonio sea de $LaTeX: 0,1$ ; que entre la segunda división de la regla y la segunda del nonio haya una diferencia de $LaTeX: 0,2$ ; y así, sucesivamente, de forma que entre la décima división de la regla y la décima del nonio haya $LaTeX: 1,0$ , es decir: la décima división del nonio coincide con la novena de la regla, según se ha dicho en la forma de construcción del nonio.

http://es.wikipedia.org/wiki/Vernier

Análisis Espectral: Determinación de la Constante de Rydberg (Fiz0311)

Contents