Formación de Imágenes por Lentes Delgadas (Fiz0312)

Formación de Imágenes por Lentes Delgadas

Objetivo

Estudiar la formación de imágenes por lentes delgadas.

Introducción

En óptica geométrica se puede definir una distancia focal por la aproximación paraxial. El sistema óptico entre objeto y pantalla se puede describir con una matriz

$LaTeX: M=\left( \begin{array}{cc} A & B \\ C & D \end{array} \right)$.

La condición para la formación de una imagen es: $LaTeX: B=0$.

Un ejemplo simple es una lente delgada entre objeto y pantalla con la matriz:

$LaTeX: M=\left( \begin{array}{cc} 1 & d_i \\ 0 & 1 \end{array} \right)\left( \begin{array}{cc} 1 & 0 \\ -1/f & 1 \end{array} \right)\left( \begin{array}{cc} 1 & d_0 \\ 0 & 1 \end{array} \right)$.

Utilizando la condición B=0 se obtiene la llamada ecuación de lentes:

$LaTeX: \frac{1}{f}=\frac{1}{d_0}+\frac{1}{d_i}$

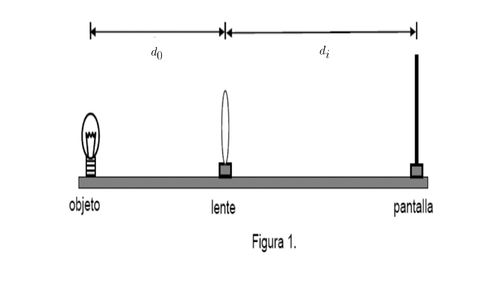
donde $LaTeX: f$ es la distancia focal de la lente, $LaTeX: d_0$ es la distancia entre el objeto y la lente, y $LaTeX: d_i$ es la distancia entre la imagen y la lente, como muestra la figura 1. Lentes con $LaTeX: f>0$ se llaman lentes positivos y lentes con $LaTeX: f<0$ se llaman lentes negativos.

Equipamiento

- Banco Óptico.

- Lentes positivas y negativas.

- Fuente de Luz (Ampolleta).

- Fuente de poder para la ampolleta.

- Pantalla.

- Regla.

Primera Parte: Distancia Focal y Magnificación de una Lente positiva.

i) Obtenga una primera medición de la distancia focal de lentes convergentes, usando el hecho que fijando las posiciones del objeto (ampolleta) e imagen (pantalla), existen dos posiciones de la lente que producen imagen.

ii) Obtenga una segunda medición de la distancia focal, graficando $LaTeX: 1/d_i$ $LaTeX: versus$ $LaTeX: 1/d_0$ para la misma lente de la medición anterior. En este conjunto de mediciones determine para cada distancia $LaTeX: s_i$ el rango de distancia en la cual la imagen tiene una calidad aceptable y asocie a este valor el error en la determinación de la posición de la imagen.

Grafique $LaTeX: 1/d_i$ $LaTeX: versus$ $LaTeX: 1/d_o$, usando los valores obtenidos, incluyendo en su gráfico las incertezas estimadas para $LaTeX: s_i$. Grafique los rangos de incerteza en los valores $LaTeX: s_i$.

iii) Usando sus datos de distancia objeto y distancia imagen encuentre la magnificación en cada posición de la lente.

Segunda Parte: Distancia Focal de una Lente Divergente

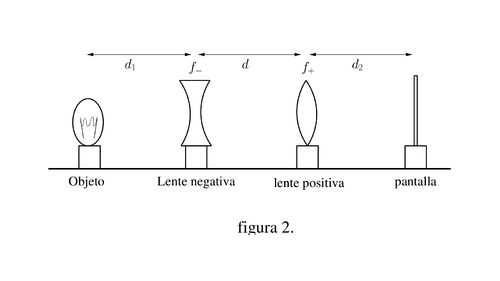
El procedimiento que ha empleado no puede utilizarse si la lente es negativa, ya que esta por si sola no puede formar una imagen real. Sin embargo, la distancia focal de una lente negativa puede calcularse si ella conforma con otra lente positiva un sistema que sea positivo. Para realizar la medición, considere el montaje óptico de la Figura 2, donde la lente positiva tiene su distancia focal conocida.

a) Arme un montaje óptico colocando entre el objeto y la pantalla una lente negativa y una lente positiva tal como se muestra en la figura 2.

c) Mueva las lentes hasta ver que se forme una imagen en la pantalla.

d) midiendo la distancia de le imagen con la lente positiva calcule usando la ecuación de lente delgada la distancia objeto de la lente positiva. Usando esta distancia objeto de la lente positiva y la distancia entre las lentes calcule la distancia imagen (imagen virtual) que debiese tener la lente negativa.

e) conociendo la distancia objeto de la lente negativa y usando el valor calculado para la distancia imagen de esta lente, calcule el foco de la lente negativa. f) Repita esta medición para otros valores, a fin de precisar su margen de error en la medición de la distancia focal de la lente negativa.

g) Calcule la matriz que describe el sistema óptico e imponga la condición de formación de imagenes para obtener el foco de la lente positiva.