Formación de Imágenes por Lentes Delgadas II (Fiz0312)

Objetivo

Estudiar la formación de imágenes por lentes delgadas.

Introducción

En óptica geométrica se puede definir una distancia focal por la aproximación paraxial. El sistema óptico entre objeto y pantalla se puede describir con una matriz

$LaTeX: M=\left( \begin{array}{cc} A & B \\ C & D \end{array} \right)$.

La condición para la formación de una imagen es: $LaTeX: B=0$.

Un ejemplo simple es una lente delgada entre objeto y pantalla con la matriz:

$LaTeX: M=\left( \begin{array}{cc} 1 & d_i \\ 0 & 1 \end{array} \right)\left( \begin{array}{cc} 1 & 0 \\ -1/f & 1 \end{array} \right)\left( \begin{array}{cc} 1 & d_0 \\ 0 & 1 \end{array} \right)$.

Utilizando la condición B=0 se obtiene la llamada ecuación de lentes:

$LaTeX: \frac{1}{f}=\frac{1}{d_0}+\frac{1}{d_i}$

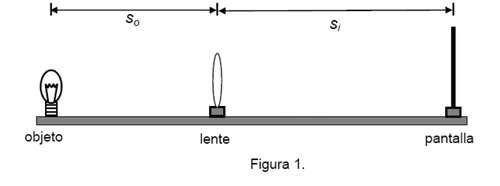
donde $LaTeX: f$ es la distancia focal de la lente, $LaTeX: d_0$ es la distancia entre el objeto y la lente, y $LaTeX: d_i$ es la distancia entre la imagen y la lente, como muestra la figura 1. Lentes con $LaTeX: f>0$ se llaman lentes positivos y lentes con $LaTeX: f<0$ se llaman lentes negativos.

Equipamiento

- Banco Óptico.

- Lentes positivas y negativas.

- Fuente de Luz (Ampolleta).

- Fuente de poder para la ampolleta.

- Pantalla.

- Regla.

Tercera Parte: Telescopio Astronómico Simple

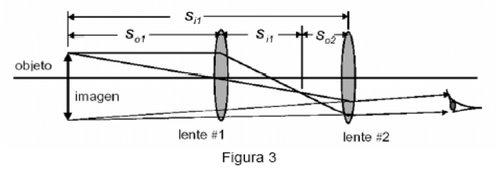
Un telescopio astronómico está formado por dos lentes convexas de distancias focales $LaTeX: f_{ab}$ (lente #1) y $LaTeX: f_0$ (lente #2). El diagrama de rayos para este experimento (se muestra en la figura 3) indica que la imagen está en el mismo plano que el objeto. Al estar la imagen en el mismo plano que el objeto, es posible determinar la distancia a la imagen virtual. Para este experimento se supone que las lentes son delgadas en comparación a las otras distancias involucradas. Por esta razón, se puede usar la ecuación 1 para lentes delgadas.

La magnificación de un sistema de dos lentes es igual al producto de las magnificaciones de las lentes individuales.

Para medir la magnificación de su telescopio, siga el siguiente procedimiento:

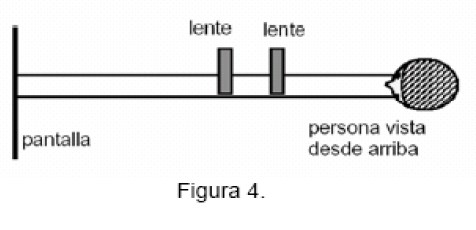
i) Ponga el papel cuadriculado incluido en la guía sobre la pantalla, usando clips. El cuadriculado en la pantalla actúa como objeto.

ii) La lente de mayor distancia focal es el objetivo (la más cercana al objeto). La lente de menor distancia focal es el ocular (la más cercana al ojo). Ponga las lentes cerca de un extremo del banco óptico y ponga la pantalla en el otro extremo. Ver figura 4.

iii) Enfoque la imagen del objeto (el cuadriculado en la pantalla), moviendo el lente objetivo (el más cercano al objeto). Para mirar la imagen, usted debe acercar un ojo al lente ocular.

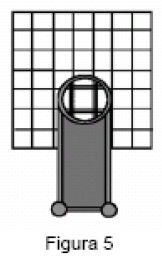
iv) Elimine el paralaje moviendo la lente ocular hasta que la imagen está en el mismo plano que el objeto (pantalla). Para observar el paralaje, abra ambos ojos y mire la imagen a través de los lentes, de modo tal que un ojo vea la imagen y el otro directamente al objeto, por fuera de los lentes (ver figura 5). Las líneas de la imagen (lineas sólidas de la figura 5) se superponen a las lineas del objeto (se muestran punteadas en la figura 5).

v) Mueva su cabeza hacia adelante y hacia atrás, arriba y abajo. Al mover la cabeza, las líneas de la imagen se mueven relativas a la del objeto, debido al paralaje. Para eliminar el paralaje, mueva el lente ocular hasta que las lineas del objeto y la imagen no se muevan unas con respecto de las otras al mover la cabeza. Cuando no hay paralaje, las lineas en el centro del lente parecen pegadas a las del objeto.

vi) Habiendo eliminado el paralaje, la imagen virtual se encuentra en el mismo plano que el objeto. Anote las posiciones de los lentes.

vii) Mida la magnificación del telescopio, contando el número de cuadrados en el objeto que corresponden a un cuadrado de la imagen. Para hacer esto, debe mirar la imagen a través del telescopio con un ojo, mientras el otro mira directamente al objeto. Anote la magnificación observada.

viii) Retire la pantalla y mire a través del lente un objeto distante, tal como una regla en el lado opuesto de la sala. Elimine el paralaje y determine la magnificación. Al observar con el telescopio un objeto ubicado ubicado muy lejos, la magnificación es el cuociente entre las distancias focales de los lentes usados. Verifique si esto se cumple para su telescopio.