Formación de Imágenes por Lentes Delgadas II (Fiz0312)
Objetivo
Estudiar la formación de imágenes por lentes delgadas.
Introducción
En óptica geométrica se puede definir una distancia focal por la aproximación paraxial. El sistema óptico entre objeto y pantalla se puede describir con una matriz
La condición para la formación de una imagen es: .
Un ejemplo simple es una lente delgada entre objeto y pantalla con la matriz:
Utilizando la condición B=0 se obtiene la llamada ecuación de lentes:
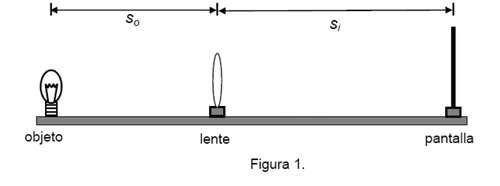
donde es la distancia focal de la lente,
es la distancia entre el objeto y la lente, y
es la distancia entre la imagen y la lente, como muestra la figura 1.
Lentes con
se llaman lentes positivos y lentes con
se llaman lentes negativos.
Equipamiento
- Banco Óptico.
- Lentes positivas y negativas.
- Fuente de Luz (Ampolleta).
- Fuente de poder para la ampolleta.
- Pantalla.
- Regla.