Ley de Stefan-Boltzmann (Alta temperatura) (Fiz0211)

Ley de Stefan-Boltzmann (Alta temperatura)

Objetivo

- Introducir experimentalmente el concepto de radiación térmica.

- Comprobar la Ley de Stefan-Boltzmann para altas temperaturas.

Materiales

- Sensor / detector de radiación (consulte especificaciones de la columna de temocuplas (Thermopile specifications) en página web de laboratorio; en ingles).

- Óhmetro (consulte manual de operación del “multimetro”)

- Voltímetro ($LaTeX: 0V-12 V$) (consulte manual de operación del “multimetro”)

- Lámpara de Stefan-Boltzmann (consulte manual de instrucción lámpara de Stefan-Boltzmann TD-8555 (en la página web del laboratorio; en ingles).

- Milivoltímetro (consulte manual de operación del “multimetro”)

- Amperímetro ($LaTeX: 0A-3 A$); (consulte manual de operación del “multimetro”)

- Termómetro (¿Cómo funciona un termómetro? ¿Qué principios físicos se pueden aprovechar para la construcción de un termómetro?)

Introducción

La ley de Stefan-Boltzmann relaciona $LaTeX: R$, la potencia por unidad de área radiada por un objeto, a $LaTeX: T$, la temperatura absoluta del objeto. La ecuación es:

$LaTeX: R = \sigma \cdot T^4$

, con $LaTeX: \sigma=5.6703 \cdot 10^{-8} W/(m^2K^4)$

En este experimento, se harán medidas de la potencia por unidad de área emitida por un objeto caliente, llamada la lámpara de Stefan-Boltzmann, a varias temperaturas. De los datos obtenidos deberá ser capaz de verificar si la potencia radiada es realmente proporcional a la cuarta potencia de la temperatura.

La mayoría de la energía térmica emitida por la lámpara viene del filamento. La temperatura del filamento puede ser determinada usando los datos que se dan en el procedimiento de la lámpara de Stefan Boltzmann.

Procedimiento

IMPORTANTE: El voltaje en la lámpara no deberá exceder $LaTeX: 13 V$. Voltajes mayores quemarían el filamento.

1. ANTES DE ENCENDER LA LÁMPARA, mida $LaTeX: T_{ref}$, la temperatura de la sala en unidades de Kelvin $LaTeX: [K]$, ($LaTeX: T[K]=T[°C]+273$) y $LaTeX: R_{ref}$, la resistencia del filamento de la lámpara de Stefan- Boltzmann a temperatura ambiente. Registre sus resultados

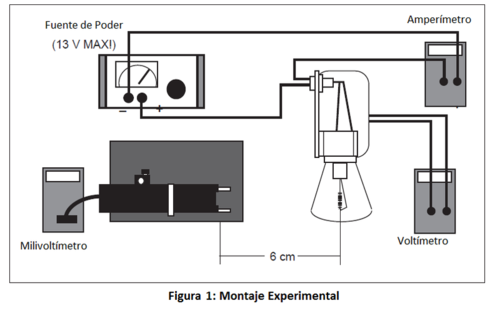
2. Arme el equipo como se muestra en la figura 3.1. El voltímetro deberá ser conectado directamente a la lámpara de Stefan-Boltzmann. El sensor deberá estar a la misma altura que el filamento, con la cara frontal del sensor aproximadamente $LaTeX: 6 cm$ alejada del filamento. El orificio de entrada de la termopila no deberá tener objetos cercanos mas que la lámpara.

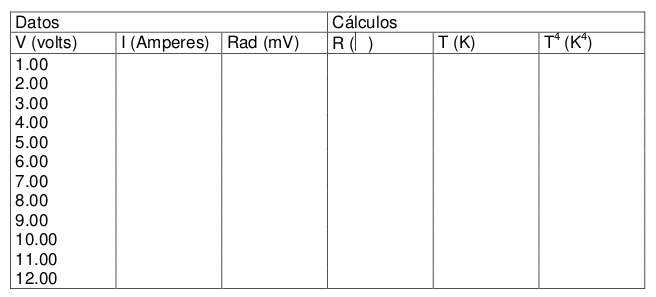
3. Encienda la fuente de poder. Ajusta el voltaje, B, para cada valor que se enlista en la tabla 1. A cada voltaje, registre $LaTeX: I$, la lectura del amperímetro, y Rad, la lectura en el milivoltímetro.

IMPORTANTE: Realice las lecturas del sensor rápidamente. Entre lecturas, coloque ambos escudos entre la lámpara y el sensor, con la cara plateada viendo a la lámpara, para que la temperatura del sensor se mantenga relativamente constante.

Datos y Cálculos

i) Calcule $LaTeX: R$, la resistencia del filamento a cada uno de los voltajes usados ($LaTeX: R=V/I$). Registre estos resultados en la tabla 1.

ii) Usa el procedimiento de la lámpara de Stefan-Boltzmann para determinar $LaTeX: T$, la temperatura del filamento a cada voltaje. Registre tus resultados en la tabla.

iii) Calcule $LaTeX: T^4$ para cada valor de $LaTeX: T$ y regístrelos en su tabla.

iv) Realice un gráfico $LaTeX: Rad$ versus $LaTeX: T^4$.

Preguntas

• ¿Cuál es la relación entre $LaTeX: Rad$ y $LaTeX: T$? ¿Esta relación se sostiene en todo el rango de medidas?

• La lámpara de Stefan Boltzmann es ideal solo para radiación de cuerpo negro. Un cuerpo negro es un cuerpo que absorbe toda la radiación que incide sobre él. ¿Es el filamento de la lámpara un cuerpo negro ideal?

• ¿Qué fuentes de radiación térmica, aparte del filamento de la lámpara, han podido influenciar tus medidas? ¿Qué efecto podría esperar que estas fuentes tengan en sus resultados?

$LaTeX: T_{ref}$ (temperatura ambiente) = _____________$LaTeX: K$ (K=^{°C + 273)

$LaTeX: R_{ref}$ (resistencia del filamento a temperatura $LaTeX: T_{ref}$)=__________$LaTeX: \Omega$

Tabla 1