Absorción de radiaciones Beta y Gamma (Fiz0311)

Absorción de radiaciones Beta y Gamma

Objetivo

- Investigar la absorción de radiaciones beta y gamma.

- Medir el coeficiente de absorción lineal de la radiación beta $LaTeX: Sr90$ en aluminio y el “mass absorption coefficient” de la radiación gamma de Co-60 en plomo.

Materiales

- Contador Geiger-Müller

- Fuentes de Radiación

- Láminas de aluminio y plomo

Radiación

Los físicos Pierre y Marie Curie llevaron a cabo gran parte de los descubrimientos básicos que sentaron las bases de una nueva área de la física: la radioactividad. Después de muchos años de investigación, estos científicos identificaron tres tipos de partículas resultantes de procesos radioactivos (radiación). Estos son: Alfa, Beta y Gamma. Las partículas alfa son núcleos de helio ($LaTeX: He^{++}$) y generalmente son detenidas por una hoja de papel, las partículas beta son electrones rápidos (se mueven a velocidades relativistas) y son detenidas por láminas de aluminio y la radiación gamma son ondas electromagnéticas (fotones de longitud de onda mas corta que rayos-x) que sólo pueden ser detenidas con un bloque de plomo.

Como se puede detectar: Contador Geiger-Muller

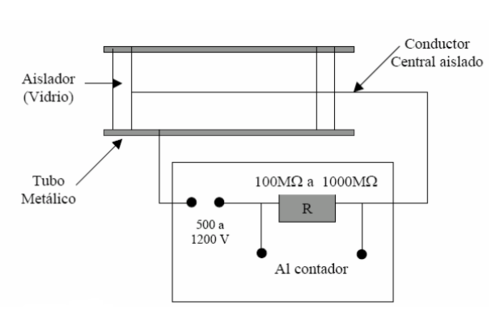
El C.G.M. está formado por un tubo metálico herméticamente cerrado, en cuyo interior se ubica un conductor aislado (filamento de tungsteno), en la misma dirección del eje del tubo.Ese filamento es el ánodo. El cátodo es una capa fina de acero inoxidable que cubre la cara interior del cilindro y que sirve de cátodo. El cátodo está conectado a la tierra. En el interior del tubo se encuentra el gas argón a una presión de $LaTeX: 260 mmHg$ (de tal forma que normalmente no conduzca electricidad), mezclado con algunos vapores orgánicos.

Sin embargo, si una partícula radiactiva golpea el tubo se producirá la ionización del tubo momentáneamente, provocando una corriente a través de los electrodos.

Para que pueda circular una corriente a través de los electrodos es necesario aplicar una cierta diferencia de potencial entre ellos (como lo muetra la figura 1). La tensión debe elegirse de manera de que no se produzca descarga espontánea. Una resistencia de $LaTeX: 100 M\Omega$ a $LaTeX: 1000 M\Omega$ limita la corriente en caso de producirse una descarga a través del gas enrarecido.

Figura 1: Contador.

El pulso de corriente provocado al incidir la partícula ionizante, ocasiona una diferencia de potencial en la resistencia que hace bajar la tensión entre el conductor central y las paredes del tubo, y por lo tanto la descarga cesa. A continuación la tensión adquiere nuevamente su valor inicial. Después de transcurrido el tiempo necesario para este proceso (tiempo muerto) el tubo se encuentra preparado para recibir nuevas partículas.

La adición de vapores orgánicos como Formiato de Etilo, Bromo o Cloro tiene por objeto:

a) Evitar que los iones positivos lleguen al cátodo con la energía suficiente para arrancar de él mas electrones que generen pulsos de descargas.

b) Absorber fotones emitidos por átomos excitados que vuelven a su estado fundamental, los que podrían también generar este tipo de pulsos.

Parte I: Curva característica de un Tubo Geiger Müller

Introducción

Para el funcionamiento del tubo contador tiene gran importancia la curva característica. Se llama así a la gráfica que representa la función entre el número de impulsos de descarga(producidos por la misma fuente y en el mismo intervalo de tiempo) y la tensión aplicada al tubo.

Procedimiento

1.- Monte el tubo G.M. en su soporte y ubique una fuente de $LaTeX: Co-60$ de $LaTeX: 1 \mu Ci$ a unos $LaTeX: 2 cm$ de él.

NOTA: Asegúrese que la fuente NO esté con la etiqueta hacia el Tubo.

2.- Aumente gradualmente la diferencia de potencial entre los electrodos del tubo hasta que comiencen a ser detectados los pulsos de corriente. Realice las mediciones hasta el voltaje máximo de $LaTeX: 1100 V$.

3.- Para disminuir los efectos del azar, característico en todos los procesos de desintegración espontánea de la materia, determine el conteo por segundo observando durante 1 o 2 minutos, las partículas detectadas.

PRECAUCIÓN: La diferencia de potencial sobre los electrodos del tubo no deben sobrepasar los 1100 V, para evitar daños irreparables en el tubo

4.- Haga un gráfico de potencial aplicado versus número de cuentas por seg.

Análisis

• A partir de la curva obtenida, explique que sucede en la primera parte de la curva (ascenso). ¿Qué sucede con el funcionamiento del tubo contador en esta zona?.

• A partir de la curva obtenida, explique que sucede en la segunda parte de la curva (Plateau). ¿Qué sucedería con el tubo mas allá de esta zona?.

• Según lo observado en la curva, ¿Cuál es la zona mas apropiada para el funcionamiento del tubo?. Fundamente su respuesta.

• Hable con el profesor o ayudante antes de seguir.

Parte II: Tiempo Muerto del Contador Geiger Müller

Introducción

Cuando una partícula ha provocado la ionización del gas en el interior del tubo G.M, se produce un intervalo de tiempo llamado “ tiempo muerto”. Durante éste intervalo el tubo no reacciona al paso de otras partículas por su interior. Entonces, cuando el número de cuentas es muy alto el tiempo muerto impide que veamos todas las partículas que ingresan al tubo.

Para medir el tiempo muerto hay que comparar el número de cuentas por segundo con dos fuentes juntas ($LaTeX: R_{(a+b)}$) con el número de cuentas por segundo con los dos fuentes separadas ($LaTeX: R_a, R_b$). En este caso el tiempo muerto es dado por,

$LaTeX: T_m=\frac{R_a+R_b-R_{(a+b)}}{2R_aR_b} \qquad\qquad\qquad (1)$

Procedimiento

1. Ubique dos fuentes de $LaTeX: 5.0 \mu Ci$ de $LaTeX: Cs-137$ a una distancia tal que el contador obtenga más de 10.000 cuentas por minuto.

2. Realice una buena medición de conteo. Este es $LaTeX: R_(a+b)$.

3. Saque una de las fuentes (sin mover la otra) y haga una medición de la tasa de conteo de la otra. Esta es $LaTeX: R_a$.

4. Reponga la fuente que sacó en su posición original y saque la otra. Esta es $LaTeX: R_b$.

5. Usando la ecuación (1) calcule el tiempo muerto del contador.

Nota: obtenga todas las tasas de conteo en las mismas unidades. El tiempo muerto debe ser unos centenares de microsegundos.

Corrección de pérdidas por Tiempo Muerto

Llamemos “t” (seg.) al intervalo de tiempo entre la detección de una partícula y el instante en que se ha recuperado el tubo G.M. y está listo para una nueva detección. Esto quiere decir que por cada detección registrada, se pierden “t” seg. Entonces si la tasa de conteo observada es de $LaTeX: n$ cuentas por segundo, el tiempo perdido por segundo es $LaTeX: n \cdot t$. Luego el tiempo útil de conteo por segundo es:

$LaTeX: \mbox{Tiempo util} = 1-n \cdot t \mbox{ (seg)}$

El conteo observado y el número real de partículas que llegaron al contador deben estar en la misma razón que el tiempo útil y el tiempo total. Si designamos por $LaTeX: N$ al número corregido por segundo, se tiene:

$LaTeX: \frac{N}{n}=\frac{1}{1-n \cdot t}$

Parte III: Relación entre Intensidad de Radiación y Distancia al Punto Origen de ella

Procedimiento

Se denomina “Background” a la radiación que es posible detectar con un contador G.M, sin que exista una fuente radiactiva. Siempre está la posibilidad de que haya pequeñas cantidades de algún elemento radioactivo ( $LaTeX: ^{14}C$, $LaTeX: ^{40}K$, etc.) en el ambiente.

1. Antes de comenzar las mediciones es conveniente poder apreciar que tan bajo es el “Background”, conecte el G.M y déjelo funcionando por un lapso de unos $LaTeX: 10 min$., y luego calcule las cuentas por minutos.

2. Coloque el tubo G.M en su soporte en posición vertical, y la fuente de radiación en la ranura más distante del tubo.

3. Determine el número de partículas detectadas en cierta unidad de tiempo.

4. Comience a variar la distancia disminuyéndola.

El tiempo de conteo en 3 y 4 debería ser suficiente para obtener un error estándar menor que 2% ó 5 minutos, cualquiera que sea más corto.

5. Confeccione un gráfico con los valores obtenidos y sus errores (vea el apéndice) del punto anterior.

Análisis

• Trate de estimar una relación matemática que represente los datos medidos en la experiencia. Suponga que el número de cuentas caiga con una curva de la forma $LaTeX: x^n$, donde $LaTeX: x$ es la distancia de la fuente. Encuentre el valor (con error) de $LaTeX: n$ utilizando la teoría de mínimos cuadrados. (Ayuda: ¿Cuál es la pendiente de un gráfico de tipo log-log?).

• ¿Cuál valor de n es esperado? Si su valor no corresponde explique porqué. (Ayuda: Considere el largo del contador.)

• ¿Qué sucede cuando la distancia entre la fuente radiactiva y el tubo contador es muy pequeña? (pocos milímetros). Explique.

Parte IV: Absorción de radiaciones Beta y Gamma

Objetivo

Investigar la absorción de radiaciones beta y gamma. Medir el coeficiente de absorción lineal de la radiación beta $LaTeX: Sr-90$ en aluminio y el “mass absorption coefficient” de la radiación gamma de $LaTeX: Co-60$ en plomo.

Introducción

La relación entre la intensidad de radiación después de atravesar un material es:

$LaTeX: I=I_0 \cdot e^{- \mu x} \qquad\qquad\qquad (1)$

Donde $LaTeX: x$ es el espesor del material y $LaTeX: \mu$ es el coeficiente de absorción lineal. La distancia de absorción es igual a $LaTeX: 1/\mu$.

A veces se escribe la ec.(1) en otra forma:

$LaTeX: I=I_0 \cdot e^{- (\mu/\rho)\rho x} \qquad\qquad\qquad (2)$

Donde $LaTeX: \mu /\rho$ se llama “mass absorption coefficient”. Se encuentran los valores del “mass absorption coefficient” para varios elementos en tablas en la siguiente dirección:

http://physics.nist.gov/PhysRefData/XrayMassCoef/tab3.html

Procedimiento

Monte el tubo G-M en su soporte y haga una medición buena (con un error Standard de ∼ 5%) del número de cuentas por minuto en ambiente. (Ayuda: La ecuación que representa la distribución de mediciones del número de cuentas de una fuente radioactiva es la distribución de Poisson. En este caso la desviación Standard,

$LaTeX: \delta x= (\Sigma/n)^{1/2}$

Donde $LaTeX: \Sigma$ es el promedio y $LaTeX: n$ es el número de mediciones

Parte I

1.- Ubique la fuente de $LaTeX: Sr-90$ en la tercera muesca del soporte. Haga una medición aproximada de las cuentas por minuto sin lámina de absorción.

2.- Mida las cuentas por minuto en una lámina de plomo. ¿Es más que el ambiente?

3.- Repita para las láminas de $LaTeX: 849 mg/cm^2$ de aluminio y $LaTeX: 4.5mg/cm^2$ de aluminio.

4.- Ubique una fuente de $LaTeX: Co-60$ en la tercera muesca del soporte. Realice una medición aproximada de las cuentas por minuto sin lámina de absorción.

5.- Luego mida las cuentas por minuto usando una lámina de 8$LaTeX: 49 mg/cm^2$ de aluminio. ¿Es mas que el ambiente?.

Pregunta: ¿Qué se puede concluir acerca de las radiaciones de las dos fuentes?

Nota: En las partes II, III y IV el tiempo de conteo debería ser suficiente para obtener un error standard menor que el 2% ó 5 minutos, cualquiera que sea mas corto.

Parte II: Medir la distancia de absorción $LaTeX: (1/\mu)$ de las partículas beta de $LaTeX: Sr-90$ en aluminio.

Con láminas adecuadas y usando un método gráfico, encuentre el valor de la distancia de absorción $LaTeX: (1/\mu)$ de las partículas beta de aluminio.

Parte III: Medir la “mass absorption coefficient ($LaTeX: \mu/\rho$)” en plomo de los rayos gammas emitidos por la fuente de $LaTeX: Co-60$.

Con láminas adecuadas y usando un método gráfico encuentre el valor de la “mass absorption coefficient” de los rayos gamma.

Se puede encontrar un gráfico del “mass absorption coefficient” v/s energía del fotón en la página web:

http://physics.nist.gov/PhysRefData/XrayMassCoef/ElemTab/z82.html

Parte IV: (Opcional) Investigar sobre la radiación de la fuente de $LaTeX: Co-60$

1.- Mida la tasa de conteo por la fuente $LaTeX: Co-60$ a través de las láminas de aluminio

comenzando con la lámina de $LaTeX: 4.15 mg/cm^2$ hasta la más gruesa.

2.- Realice un gráfico de cuentas contra $LaTeX: \rho x$ (de igual forma que antes).

3.- Incluya en el gráfico los resultados de la parte 2.

4.- ¿Qué espera de éste resultado?. Explique la curva del gráfico.

Apéndice: Estadísticas de la Radiación

La emisión de la radiación es un proceso aleatorio que sigue las estadísticas de Poisson. Una propiedad muy útil de las estadísticas de Poisson es que la desviación standard es igual a la raíz del promedio,

$LaTeX: \Sigma=\sqrt{\bar{x}}$

Esta relación la podemos usar para calcular el error en nuestros mediciones.

Por ejemplo, si se mide las cuentas de una fuente por 10 minutos y obtiene 5000 cuentas, ¿cuáles son las cuentas por minuto?. El promedio de las cuentas por minuto $LaTeX: = 5000/10=500$ cuentas por minuto.

El error está dado por,

$LaTeX: \delta x=\frac{\Sigma}{\sqrt{n}}=\sqrt{\frac{\bar{x}}{n}}$

donde $LaTeX: n$ es el numero de mediciones de las cuentas por minuto. En este caso tenemos una medición de 10 minutos, es equivalente a 10 mediciones de un minuto, entonces $LaTeX: n=10$ y $LaTeX: \delta x=7$. Las cuentas por minuto son $LaTeX: 500 \pm 7$.