Calor Específico de un Metal (Fis 152)

Calos Expecífico de un Metal

Objetivos

- Determinar el calor específico del Cobre (Cu).

- Comprobar experimentalmente la ley cero de la Termodinámica.

Introducción

Diferentes sustancias requieren diferentes cantidades de calor para producir un cambio dado en su temperatura. Por ejemplo, para incrementar la temperatura de $LaTeX: 1 kg$ de agua en una cantidad $LaTeX: \Delta T$ de temperatura se requiere alrededor de 10 veces más calor que para incrementar en esta misma cantidad $LaTeX: \Delta T$ la temperatura de $LaTeX: 1 kg$ de cobre. Este comportamiento de los materiales es caracterizado cuantitativamente por el calor específico, que es la cantidad de calor necesaria para incrementar la temperatura de $LaTeX: 1 gr$ de sustancia en 1°C. Así, el agua tiene un calor específico de mayor valor que el cobre.

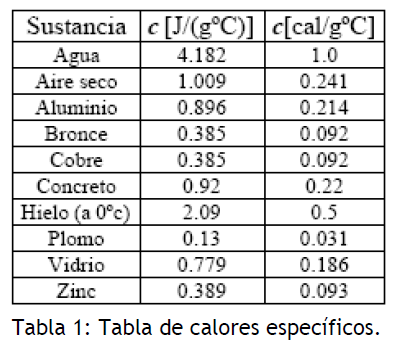
El calor específico de un material es característico para cada sustancia y depende de su estructura interna. Como puede ser visto de la definición, el calor específico de una sustancia dada puede ser determinado mediante la entrega de una cantidad de calor conocida a una cantidad de masa determinada de la sustancia y con un apropiado registro del cambio en su temperatura. El propósito de este experimento es determinar el calor específico de un material en particular mediante los métodos de calorimetría.

Teoría

Una variación $LaTeX: \Delta T$ en la temperatura de una sustancia es proporcional a la cantidad de calor $LaTeX: Q$ que se agrega o extrae de esta, o sea:

$LaTeX: Q \propto \Delta T$

Escrito en forma de ecuación

$LaTeX: Q = C \cdot \Delta T \qquad\quad\qquad (1)$

Donde la constante de proporcionalidad $LaTeX: C$ es llamada capacidad calorífica de la sustancia.

Sin embargo la cantidad de calor requerido para cambiar la temperatura de un objeto es también proporcional a la masa de este, por lo tanto es conveniente definir la cantidad llamada capacidad calorífica específica $LaTeX: c$ (o calor específico)

$LaTeX: c=\frac{C}{m} \qquad\quad\qquad (2)$

que es la capacidad calorífica por unidad de masa de la sustancia. Así, la ecuación (1) puede ser escrita como:

$LaTeX: Q = m \cdot c \cdot \Delta T \qquad\quad\qquad (3)$

Donde el calor específico es la cantidad de calor (en calorías) necesaria para incrementar la temperatura de 1 gramo de sustancia en 1 grado Celsius.

De hecho, la caloría es la unidad de calor definida como la cantidad de calor requerido para incrementar la temperatura de $LaTeX: 1 gr$ de agua en 1°C. Por definición, el agua tiene un calor específico de $LaTeX: 1 cal/g^{\circ}C$.

$LaTeX: Q = \frac{\Delta Q}{m \cdot \Delta T}=1cal/gr^{\circ}C$

En la tabla mostrada a continuación se presentan los valores de los calores específicos para algunos materiales.

El calor específico de un material puede ser determinado experimentalmente midiendo el cambio de temperatura que presenta una determinada masa del material al entregarle una cierta cantidad de calor. Esto puede ser realizado indirectamente por un procedimiento de calorimetría conocido como el método de mezclas. Varias sustancias a diferentes temperaturas se ponen en contacto térmico, las sustancias calientes entregan calor a las sustancias frías hasta que todas las sustancias alcanzan una temperatura de equilibrio común.

Si el sistema está aislado de manera que no pueda intercambiar calor con sus alrededores, por conservación de energía, la cantidad de calor que pierden las sustancias calientes es la misma que ganan las sustancias frías.

$LaTeX: |Q_c| = |Q_f| \qquad\quad\qquad (4)$

En este experimento, agua caliente es añadida a un calorímetro (vaso térmico) el cual contiene una barra metálica, luego se agita el calorímetro por unos segundos hasta que el sistema alcanza el equilibrio térmico. Note que la función del calorímetro es aislar el sistema para disminuir las pérdidas de calor. Sin embargo, su capacidad calorífica es desconocida, por lo tanto esta debe ser inicialmente medida.

Experimento

I. Medición de la Capacidad Calorífica del Calorímetro

Equipamiento Requerido:

- 1 calorímetro

- 1 termómetro de mercurio

- 1 vaso precipitado de $LaTeX: 250 ml$

- 1 calentador eléctrico de $LaTeX: 600 W$

- 1 guante térmico

- Balanza del laboratorio

PRECAUCIÓN

La superficie del calentador puede llegar a temperaturas cercanas a los 350 °C, por ello debe tener mucha precaución al manipular este calentador.

Recuerde utilizar siempre el guante térmico para manipular el vaso precipitado cuando esté a una temperatura elevada.

Procedimiento

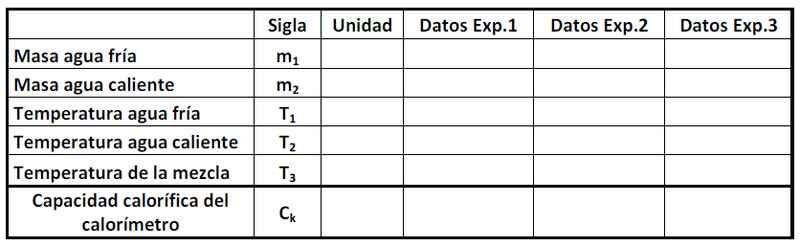
1. Añada al calorímetro $LaTeX: 100 ml$ de agua a temperatura ambiente previamente pesada. Observe la lectura del termómetro y cuando esta

se estabilice, registre su valor como $LaTeX: T_1$ (Temperatura inicial sistema calorímetro más agua) en la tabla que se muestra más adelante.

2. Caliente en un vaso precipitado $LaTeX: 100 ml$ de agua a una temperatura aproximada de 50°C y registre esta temperatura como $LaTeX: T_2$. Vierta esta cantidad de agua caliente (previamente pesada) en el calorímetro con agua y ciérrelo. Homogenice la temperatura del agua agitando suavemente el calorímetro. Espere unos segundos hasta que la temperatura llegue a un valor estacionario y registre esta temperatura como $LaTeX: T_3$.

3. Luego de anotar los datos en la tabla, determine la capacidad calorífica del calorímetro ($LaTeX: C_k$) aplicando la ley de la conservación de la energía.

. Realice el experimento anterior tres veces.

Si el valor de $LaTeX: C_k$ no tiene una dispersión excesiva, promedie los valores y anote como error la desviación estándar. En caso contrario repita sus medidas con cuidado y estudie donde puede estar el problema.

Nota: El valor experimental de $LaTeX: C_k$ debe ser reportado como:

$LaTeX: C_k=\bar{x} \pm \sigma$

La desviación estándar ($LaTeX: /sigma$) está dada por:

$LaTeX: \sigma=\sqrt{\frac{1}{N}\sum_{i=1}^N(x_i-\bar{x})^2}$

Donde $LaTeX: N$ es el número de mediciones, $LaTeX: x_i$ la medición i-ésima y $LaTeX: \bar{x}$ es el promedio de las $LaTeX: N$ mediciones.

II. Determinación del Calor Específico de un Sólido

Equipamiento Requerido

- 1 calorímetro

- 1 termómetro de de mercurio

- 1 vaso precipitado de $LaTeX: 250 ml$

- 1 calentador eléctrico de $LaTeX: 600 W$

- 1 trozo de Cobre (barra metálica color rojizo)

- 1 guante térmico

Procedimiento

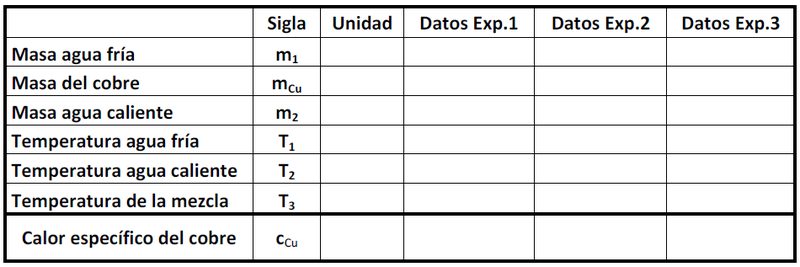
1. Medir la masa del metal y depositarlo en el calorímetro.

2. Añadir al calorímetro $LaTeX: 100 ml$ de agua a temperatura ambiente previamente pesada. Observe la lectura del termómetro y cuando se estabilice, registre su valor como $LaTeX: T_1$ (Temperatura inicial sistema calorímetro, agua y barra de cobre) en la tabla que se muestra más adelante.

3. Caliente en un vaso precipitado $LaTeX: 100 ml$ de agua a una temperatura aproximada de 50°C y registre esta temperatura como $LaTeX: T_2$. Vierta esta cantidad de agua caliente (previamente pesada) en el calorímetro y ciérrelo. Homogenice la temperatura de la mezcla agitando suavemente el calorímetro. Espere unos segundos hasta que la temperatura llegue a un valor estacionario y registre esta temperatura como $LaTeX: T_3$.

4. Luego de anotar los datos en la tabla, determine el calor específico del cobre ($LaTeX: c_{Cu}$) aplicando la ley de la conservación de la energía.

5. Realice el procedimiento anterior tres veces.

Si el valor de $LaTeX: c_{Cu}$ no tiene una dispersión excesiva, promedie los valores y anote como error la desviación estándar. En caso contrario repita sus medidas con cuidado y estudie donde puede estar el problema.

Preguntas

1) ¿Qué expresa la ley cero de la termodinámica y en que parte de este experimento está presente?

2) ¿Cuál es el valor experimental reportado por su grupo para la capacidad calorífica del calorímetro $LaTeX: C_k$?

3) ¿Cuáles son las posibles fuentes de error en la medición de $LaTeX: C_k$?

4) ¿Cuál es el valor experimental reportado por su grupo para el calor específico del cobre $LaTeX: c_{Cu}$?

5) Probablemente el valor de $LaTeX: c_{Cu}$ obtenido por su grupo tiene un gran porcentaje de error en comparación con el valor reportado en la tabla 1. Identifique las posibles fuentes de error en la medición de $LaTeX: c_{Cu}$.

6) ¿Qué aspectos del procedimiento experimental podrían ser mejorados para obtener un valor del calor específico del metal con un menor porcentaje de error?