Ondas Estacionarias en una Cuerda (Fiz109 DS)

Ondas Estacionarias en una Cuerda

Objetivo

Observar las ondas estacionarias en una cuerda tensa y mediante el análisis y medición de algunos parámetros importantes, involucrados en este fenómeno.

Materiales

- Amplificador de Potencia PASCO CI-6502

- Computador PC con interfaz PASCO

- Cuerda

- Masas

- Parlante

- Programa DATA STUDIO

Introducción

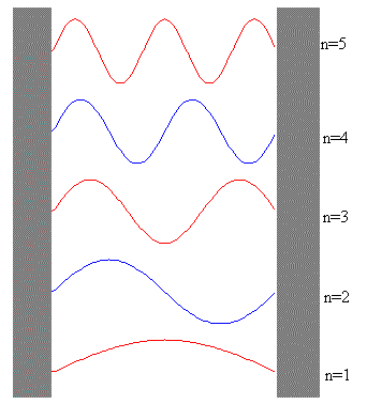
Las ondas estacionarias no son ondas de propagación sino los distintos modos de vibración de una cuerda, una membrana, etc. Cuando dos trenes de onda de la misma frecuencia, velocidad y amplitud, viajan en sentidos opuestos, la superposición de ellos da lugar a ondas estacionarias. Una de las características más importantes de estas ondas es el hecho de que la amplitud de la oscilación no es la misma para diferentes puntos, sino que varía con la posición de ellos.

Hay puntos que no oscilan, es decir, tienen amplitud cero; dichas posiciones se llaman nodos.

También hay puntos que oscilan con amplitud máxima; esas posiciones se llaman antinodos.

Figura 1: Ondas Estacionarias con su respectivo número de armónicos (n).

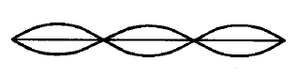
En una cuerda fija en ambos extremos, se pueden formar ondas estacionarias de modo que siempre los puntos extremos son nodos. La cuerda puede oscilar con distintas formas denominadas modos de vibración, con nodos entre sus extremos, de tal manera que las longitudes de onda $LaTeX: \lambda$ correspondientes a las ondas estacionarias cumplen con la relación:

$LaTeX: n\frac{\lambda}{2}=L \qquad\qquad\qquad (1)$

donde $LaTeX: L$ es el largo de la cuerda y $LaTeX: n = 1, 2, 3,...$ son los armónicos.

Sabemos que la velocidad de propagación de una onda en un medio homogéneo, esta dado por:

$LaTeX: V = \lambda \cdot f \qquad\qquad\qquad (2)$

Siendo $LaTeX: f$ la frecuencia de la vibración. Por otra parte, la velocidad de propagación de una onda transversal en una cuerda, está dada por:

$LaTeX: V=\sqrt{\frac{T}{\mu}} \qquad\qquad\qquad (3)$

Donde $LaTeX: T$ es la tensión de la cuerda y $LaTeX: \mu$ su densidad lineal. De las expresiones (1), (2) y (3) Ud. puede deducir que:

$LaTeX: f_n=\frac{nV}{2L}=\frac{n}{2L}\sqrt{\frac{T}{\mu}} \qquad\qquad\qquad (4)$

Esta expresión da todas las frecuencias naturales de oscilación de la cuerda, o dicho de otra forma, las frecuencias correspondientes a los distintos modos de vibración de la cuerda.

Para $LaTeX: n=1$, se obtiene $LaTeX: f_1 =V/2L$ , siendo el primer armónico o frecuencia fundamental de la cuerda. Y para $LaTeX: n = 2,3,...$ se obtienen $LaTeX: f_2, f_3,,.....,$ llamados armónicos.

Cuando una cuerda se pone en vibración, las oscilaciones se amortiguan y se reducen gradualmente a cero. Trate Ud. de explicar las principales causas de este amortiguamiento investigando las posibles disipaciones de energía.

Es posible superar los efectos del amortiguamiento comunicando energía al sistema mediante una fuerza propulsora externa. Si la frecuencia de ésta es muy parecida a una de las frecuencias naturales de vibración de la cuerda (dada por la expresión (4)), entonces ella vibrará con esa frecuencia y con gran amplitud, fenómeno que recibe el nombre de resonancia.

Montaje Experimental

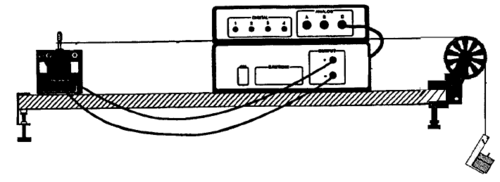
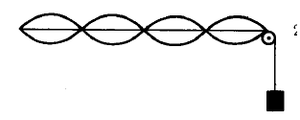
i) Conecte el parlante al amplificador de potencia (fig. 2).

ii) Ubique el parlante a una distancia de $LaTeX: 1.2 m$ aprox, de la polea.

Figura 2: Montaje Experimental.

iii) Asegúrese de que la cuerda quede enganchada en el cono plástico.

iv) Encienda el computador y llame al programa Data Studio.

Parte I : Cálculo de la Densidad Lineal de Masa de una Cuerda

1) Pese una cuerda de aproximadamente $LaTeX: 1 m$ de longitud.

2) Calcule la densidad lineal de masa de la cuerda ($LaTeX: \mu$) .

Parte II : Tensión Variable; Frecuencia y Longitud Constantes

Figura 3: Ventana del Generador de Señales.

1) Seleccione y conecte el Amplificador de Potencia (Power Amplifier) .

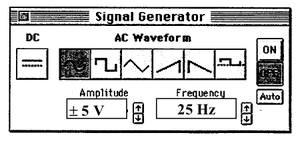
2) Aparecerá una pequeña ventana Signal Generator (Generador de Señales) (figura 3) que configura las caracteristicas del generador de señales (amplificador de potencia). Para ello ingrese $LaTeX: 5V$ para la amplitud.

3) Seleccione la forma de onda (AC Waveform) en la ventana Signal Generator.

4) Inicialmente seleccione una frecuencia entre los rangos de $LaTeX: 10$ a $LaTeX: 25 Hz$, para así poder observar la frecuencia fundamental (fig.5). Presione On para iniciar la experiencia. Una vez observada la fundamental, deberá variar los valores de la frecuencia para observar los patrones de las ondas estacionarias con que Ud.va a trabajar.

5) Mida la longitud de la sección de la cuerda que vibrará (fig.4) y registre esta longitud en la tabla 1.

Figura 5: Modo fundamental.

Figura 6.

Figura 7.

Figura 4: Ondas Estacionarias en una Cuerda.

5) Mida la longitud de la sección de la cuerda que vibrará (fig.4) y registre esta longitud en la tabla 1.

6) Ponga algunas masas(no mas de 10 golillas) en el gancho colgante hasta que la cuerda vibre en el modo fundamental .Observe, (ver fig.5). NOTA: No es necesario graficar esta frecuencia

7) Luego varíe las frecuencias hasta $LaTeX: 80 Hz$. y ajuste la cantidad de masas hasta que los nodos se vean como puntos oscuros (sin vibración). Registre las masas en la tabla 1. Ver figuras 6 y 7.(No considere la fundamental como punto a graficar)

8)Para cada medición de armónico escogido mida la longitud de onda correspondiente .

9) Pida a su profesor o a su ayudante un estroboscopio luminoso. Este dispositivo es una fuente luminosa con una lámpara de Xenón de frecuencia variable. Ajuste la frecuencia del estroboscopio hasta que vea el vibrador estacionario y observe la cuerda.

Precaución: NO cuelgue más de 12 golillas ya que puede destruir el parlante.

Tabla 1: Fuerza Variable

Frecuencia: _________________ Longitud de la Cuerda: _____________________

Tabla 1

Análisis

a) Describa el aspecto de la cuerda cuando el sistema cuerda-parlante está en resonancia.

b) Con los datos obtenidos haga un gráfico $LaTeX: T$ versus $LaTeX: 1/n^2$ .

c) Encuentre la pendiente de la curva obtenida.

d) Usando la pendiente, calcule la densidad lineal de masa de la cuerda. Registre el valor de $LaTeX: \mu$ obtenido en la tabla 3.

e) Relacione las mediciones de la longitud de onda obtenidas con el número $LaTeX: n$.

Parte II: Frecuencia Variable: Tensión y Longitud Constantes

Procedimiento

1) Ponga $LaTeX: 50 gr$ aproximadamente, de masa en el colgador y registre la tensión en la tabla 2.

2) Varíe el valor de la frecuencia en el computador hasta que la cuerda vibre a la frecuencia fundamental.

3) Ajuste el valor de la frecuencia de tal forma que la cuerda vibre con dos, tres nodos etc., cuidando que el punto de vibración sea lo mas próximo a un nodo.

Tabla 2: Frecuencia Variable

Tensión: _________________ Longitud de la Cuerda: _____________________

Tabla 2

Análisis

a) Dibuje un gráfico Frecuencia vs N° de segmentos ($LaTeX: f$ versus $LaTeX: n$)

b) Encuentre la pendiente de la curva del gráfico realizado.

c) De la pendiente calcule la densidad lineal de la cuerda, y registre este valor en la tabla 3.

d) Calcule el porcentaje de la diferencia entre éste valor y la medida directa del valor registrado en la tabla 3.

Tabla 3: Resultados

Tabla 2

Preguntas

• Al incrementar la tensión, ¿Aumenta o disminuye el número de segmentos?.Justifique.

• Al incrementar la frecuencia, ¿Aumenta o disminuye el número de segmentos?.Justifique

• Al incrementar la tensión, ¿la velocidad de la onda aumenta, disminuye o se mantiene constante?. Explique.

• Al observar la cuerda en algún modo de vibración, ¿coincide la frecuencia observada con lo que marca el estroboscopio?.Explique.

• ¿Cómo relaciona el $LaTeX: \lambda$ medido experimentalmente con el número $LaTeX: n$?. Explique.