Campo Eléctrico (Fiz0221)

Campo Eléctrico

Objetivo

Medir las líneas equipotenciales para luego calcular el campo eléctrico en tres configuraciones espaciales. Comparar los campos obtenidos con aquellos calculados por la ley de Gauss.

Materiales

- Papel conductor de Carbón

- Pila ($LaTeX: 1.5 V$)

- Lapiz con tinta conductora

- Voltimetro

Introducción

Todo cuerpo cargado eléctricamente genera un campo eléctrico en el espacio. Una carga ubicada en este campo experimentará una fuerza en la dirección de las líneas de campo. Por convención, la dirección del campo eléctrico en un punto es la dirección de la fuerza actuante sobre la carga en ese punto. Al Campo eléctrico se le asocia un potencial eléctrico.

Existe una diferencia entre el potencial eléctrico y la energía potencial. La energía potencial eléctrica de una carga en un punto determinado en un campo eléctrico, es el trabajo necesario para mover la carga desde el infinito hasta ese punto. Tal como con todas las formas de energía, la medición es en Joules. Sin embargo, el potencial eléctrico es la energía potencial por unidad de carga, o el trabajo necesario para mover una unidad de carga desde el infinito hasta el punto. Esto se mide en $LaTeX: V=Joules/Coulomb(J/C)= Volt$

Un concepto útil es la diferencia de potencial eléctrico. Esto es el trabajo necesario para mover una unidad de carga desde un punto a otro en un campo eléctrico, y es el análogo al trabajo necesario para mover un objeto desde una altura a otra en el campo gravitacional de la tierra.

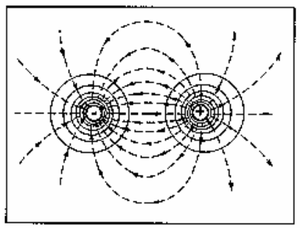
En un campo eléctrico existen muchos puntos que tienen el mismo potencial, éstos puntos son llamados Puntos Equipotenciales, y la línea que conecta esos puntos es llamada Línea Equipotencial. Las líneas de fuerza son siempre perpendiculares a las líneas equipotenciales. En este experimento el campo eléctrico será dibujado para varias configuraciones de electrodos para determinar las líneas equipotenciales y dibujar las líneas de fuerza.

Teoría

Las cargas eléctricas experimentan fuerzas debido a la presencia de otras cargas. El campo eléctrico se define como la fuerza por unidad de carga que experimenta una carga de prueba

$LaTeX: \vec{F}=q\vec{E} \qquad\qquad\qquad (1)$

Las líneas de campo eléctrico(líneas de Fuerza) se pueden pensar como la trayectoria que seguiría una carga de prueba si se suelta en un campo eléctrico. Estas se originan en las cargas positivas y terminan en las cargas negativas (una carga de prueba se considera (+) por convención).

En general, el calculo del campo eléctrico es un problema complicado, el cual muchas veces necesita ser resuelto en forma computacional. Sin embargo cuando hay altos grados de simetría en el problema, se puede usar la ley de Coulomb o la ley de Gauss, para obtener expresiones para el campo eléctrico.

Ley de Coulomb:

$LaTeX: \vec{E}=\frac{1}{4 \pi \epsilon_0} \sum_i \frac{q_i(\vec{r}-\vec{r_i})}{|\vec{r}-\vec{r_i}|^3} \qquad\qquad\qquad (2)$

Donde, $LaTeX: \frac{1}{4 \pi \epsilon_0}=8.99 \cdot 10^9 \frac{Nm^2}{C^2}$ es la constante de Coulomb.

Ley de Gauss,

$LaTeX: \int_S \vec{E} \cdot d\vec{S}=\frac{\sum Q}{\epsilon_0} \qquad\qquad\qquad (3)$

Donde $LaTeX: S$ es una superficie cerrada y $LaTeX: \sum Q$ es la carga total encerrada por $LaTeX: S$.

El campo eléctrico, en el interior de $LaTeX: S$ está relacionado con la diferencia de potencial, $LaTeX: V$,mediante:

$LaTeX: \vec{E}=-\vec{\nabla}V \qquad\qquad\qquad (4.a)$

o equivalentemente,

$LaTeX: V_{ab}=-\int_a^b \vec{E} \cdot d\vec{l} \qquad\qquad\qquad (4.b)$

Y por lo tanto tiene una magnitud igual a la derivada del voltaje y una dirección perpendicular a las líneas de igual voltaje(llamadas equipotenciales).

En este experimento los electrodos se dibujan en el papel de carbón con una tinta conductora platinada. La alta pero finita resistividad del papel carbón, permite que las equipotenciales sean fácilmente dibujables (siempre que la resistencia de entrada del voltímetro sea mayor que la resistencia del papel). De esta manera, el campo eléctrico en las dos configuraciones espaciales, se pueden obtener.

Procedimiento Experimental

1) Para este experimento use hojas de papel conductor y conecte los electrodos a la fuente de voltaje DC proporcionada.

2) Use el lápiz conductor para dibujar los electrodos en el papel de carbón. Antes de usar el lápiz debe agitarlo bien. Preocúpese que las líneas sean continuas, sin cortes o partes demasiado angostas. Deje que la tinta se seque.

3) Conecte los cables desde la pila a los electrodos. El voltaje se mide “pinchando” sobre el papel con las sondas del voltímetro, normalmente se pone sobre un electrodo y la otra sobre el punto en el cual se quiere ,medir el voltaje.

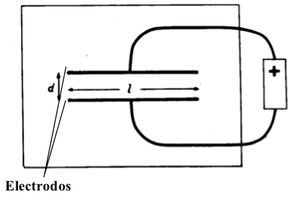
I) Placas Paralelas

Placas infinitamente largas pueden ser representadas por dos líneas paralelas en el papel de carbón. Mida el voltaje relativo a un electrodo como función de la distancia entre los electrodos ($LaTeX: d$).(Es aconsejable hacer la medición entre los puntos medios de los electrodos). La ecuación (4a) muestra que el campo eléctrico es uniforme entre los electrodos. Está de acuerdo con el campo eléctrico calculado usando la ley de Gauss.

Dibuje las equipotenciales entre las placas.¿Qué les ocurre en los extremos?. Dibuje el campo eléctrico.

II) Conductores Coaxiales

Dibuje dos círculos concéntricos con radios $LaTeX: a=1 cm$ y $LaTeX: b= 8 cm$. Esto es equivalente a dos cables coaxiales conductores infinitos perpendiculares al papel. Usando la ley de Gauss en esta configuración, muestre que el campo eléctrico varía como $LaTeX: 1/r$ donde $LaTeX: a<r<b$.

Usando la ecuación (4b), ¿cómo debiera variar el voltaje entre los electrodos como función de $LaTeX: r$?. Dibuje las equipotenciales para esta configuración.

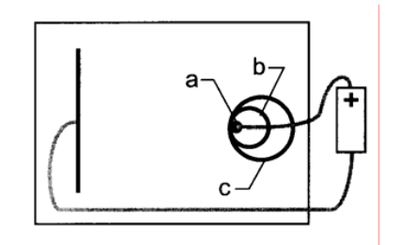
III) Punto-Plano

Dibuje solo la línea y una fuente puntual “a”. Ubique las equipotenciales. Agregue un electrodo circular “b” y nuevamente mapee las equipotenciales. Agregue un electrodo circular “c”. Repita los pasos anteriores

4) Investigue las equipotenciales y el campo eléctrico entre las dos perpendiculares entre sí. ¿Cuál es una aplicación útil de esta configuración?.¿Porqué debieran evitarse los bordes puntudos cuando se trabajo con altos voltajes?.

Si le alcanza el tiempo investigue otras configuraciones que le interesen.

Tenga presente que el papel debe ser usado de manera moderada.