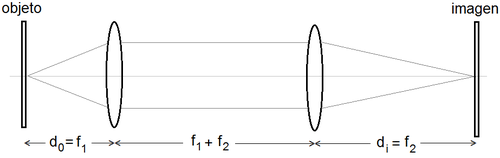Lentes Delgados (Fiz0312)
(→Introducción) |
|||
| Line 10: | Line 10: | ||
En óptica geométrica se puede definir una distancia focal por la aproximación paraxial. En el caso de lentes delgados, la formación de imágenes y la magnificación de la imagen obtenida vendrán dadas por: |
En óptica geométrica se puede definir una distancia focal por la aproximación paraxial. En el caso de lentes delgados, la formación de imágenes y la magnificación de la imagen obtenida vendrán dadas por: |
||
| − | :<center><math>\frac{1}{f}=\frac{1}{d_0}+\frac{1}{d_i}</math></center> |
+ | :<center><m>\frac{1}{f}=\frac{1}{d_0}+\frac{1}{d_i}</m></center> |
| − | :<center><math>M=-\frac{d_i}{d_0}</math></center> |
+ | :<center><m>M=-\frac{d_i}{d_0}</m></center> |
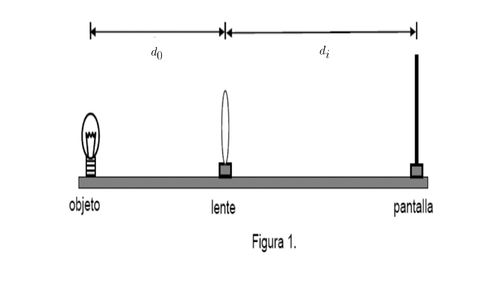
| − | donde <math>f</math> es la distancia focal de la lente, <math>d_0</math> es la distancia entre el objeto y la lente, <math>d_i</math> es la distancia entre la imagen y la lente, como muestra la figura 1. <math>M</math> corresponde a la magnificación. Lentes con <math>f>0</math> se llaman lentes convergentes y lentes con <math>f<0</math> se llaman lentes divergentes. |
+ | donde <m>f</m> es la distancia focal de la lente, <m>d_0</m> es la distancia entre el objeto y la lente, <m>d_i</m> es la distancia entre la imagen y la lente, como muestra la figura 1. <m>M</m> corresponde a la magnificación. Lentes con <m>f>0</m> se llaman lentes convergentes y lentes con <m>f<0</m> se llaman lentes divergentes. |
[[File:lablent1.jpg|center|thumb|500px|]] |
[[File:lablent1.jpg|center|thumb|500px|]] |
||
Revision as of 14:26, 22 October 2014
Contents |
Lentes Delgados
Objetivo
Estudiar la formación de imágenes por lentes delgadas.
Introducción
En óptica geométrica se puede definir una distancia focal por la aproximación paraxial. En el caso de lentes delgados, la formación de imágenes y la magnificación de la imagen obtenida vendrán dadas por:
donde es la distancia focal de la lente,
es la distancia entre el objeto y la lente,
es la distancia entre la imagen y la lente, como muestra la figura 1.
corresponde a la magnificación. Lentes con
se llaman lentes convergentes y lentes con
se llaman lentes divergentes.
Equipamiento
- Banco Óptico.
- Lentes convergentes y divergentes.
- Fuente de Luz (Ampolleta), con su correspondiente fuente de poder.
- Pantalla.
- Regla.
Primera Parte: Distancia Focal y Magnificación de una Lente positiva.
- i) Obtenga una primera medición de la distancia focal de lentes convergentes, usando el hecho que fijando las posiciones del objeto (ampolleta) e imagen (pantalla), existen dos posiciones de la lente que producen imagen. Mida
,
y
(altura de la imagen).
- ii) Obtenga una segunda medición de la distancia focal, graficando
para la misma lente de la medición anterior. En este conjunto de mediciones determine para cada distancia
Grafique
, usando los valores obtenidos, incluyendo en su gráfico las
incertezas estimadas para
. Grafique los rangos de incerteza en los valores
.
- iii) Usando sus datos
, para calcular la altura del objeto.
Segunda Parte: Distancia Focal de una Lente Negativa
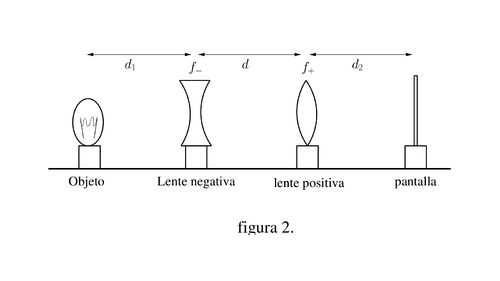
El procedimiento anterior no es util al momento de determinar la distancia focal de una lente divergente, ya que esta por si sola no puede formar una imagen real. Sin embargo, la distancia focal de una lente divergente puede calcularse si ella conforma con otra lente convergente un sistema que sea convergente. Para realizar la medición, considere el montaje óptico de la Figura 2, donde la lente convergente tiene su distancia focal conocida.
- a) Arme un montaje óptico colocando entre el objeto y la pantalla una lente negativa y una lente positiva tal como se muestra en la figura 2.
- b) Mueva las lentes hasta ver que se forme una imagen en la pantalla.
- c) Mida las distancias
,
y
. La distancia focal
se puede determinar usando las distancias medidas (
- d) Repita estas mediciones a fin de disminuir su margen de error en la medición de la distancia focal de la lente divergente.
Tercera Parte: Microscopio
Un microscopio sencillo se puede formar utilizando dos lentes convergentes como muestra la figura
donde la magnificación de esta configuración es . El objeto a mirar bajo su sencillo microscopio será su propia tarjeta PUC. Para esto, usted siga este procedimiento:
- a) Utilice primero el papel milimetrado como objeto
- b) El lente con menor distancia focal lo colocará como "objetivo" (en la posición más cercana al objeto). Coloque su objeto (papel milimetrado) en el plano focal del objetivo. A partir de esto, encuentre el plano imagen del sistema.
- c) Mida la magnificación de su microscopio a partir de las mediciones del papel milimetrado. Compare este valor con lo esperado para esta configuración óptica.
- d) Ponga la tarjeta PUC sobre el papel milimetrado en el plano objeto y observe los puntos azules en el borde de la tarjeta con su microscopio. A partir de esto, determine la distancia entre estos puntos azules utilizando el papel milimetrado como referencia.
Partes Adicionales
Usando materiales asociados a los montajes previos, y algunos recursos extra disponibles en el laboratorio, usted podría estudiar:
- 1. Construcción de un telescopio
Utilizando un objeto ubicado muy lejos () y utilizando un montaje óptico similar al microscopio; usted podria medir objetos lejanos (los cuales no puede distinguir claramente con sus ojos). Tenga presente la magnificación de su nuevo sistema al construir su telescopio.
- 2. Relación entre radio curvatura y distancia focal
Utilizando un esferómetro, usted puede medir los radios de curvatura de los lentes delgados utilizados. A partir de esto, usted puede determinar la relación entre estos radios de curvatura y la distancia focal o el índice de refracción de los lentes delgados utilizados
- 3. Aberración cromática
Utilizando filtros de distintos colores, usted podria medir las (posibles) variaciones en la distancia focal de los lentes para distintos colores. Además, a partir de esto, podría estimar la variación del índice de refracción de los lentes con respecto a las distintas longitudes de onda.
- 4. Imágenes de medios transparentes con gradientes de índices de refracción (shadowgrafia)
Utilizando una configuración similar al sistema descrito en la sección "Microscopio", usted podría apreciar gradientes en el índice de refracción en medios transparentes. En la zona donde los haces de luz son paralelos, coloque un encendedor (o algun medio transparente con gradientes en su índice de refracción) y aprecie los cambios en el plano imagen de la luz que lo atraviesa.
En esta sección, usted debe elegir al menos uno de estos fenómenos para estudiar. Debe registrar en su Acta lo que está analizando, cómo lo hace, los inconvenientes y resultados obtenidos, análisis, etc. Si usted se le ocurre algo interesante de medir, dentro del contexto del curso, puede agregarlo a la lista de “Adicionales”
