Ondas Estacionarias en 1-D (Fiz0312)

Revision as of 15:27, 15 July 2013

Ondas Estacionarias en 1-D

Objetivo

Estudiar ondas estacionarias en un medio 1-D

Introducción

El experimento consiste en el estudio de modos normales de vibración asociados a ondas estacionarias transversales y longitudinales en un medio 1-D.

Los modos normales de vibración asociados a ondas estacionarias en un medio 1-D de largo L, con ambos extremos fijos, tienen una elongación de la forma:

$LaTeX: y_n(x,t)=A\sin(k_n x) \cdot \sin(\omega_n t + \varphi)$

tanto para ondas transversales como para ondas longitudinales, cuyo número de onda viene dado por:

$LaTeX: k_n = \frac{\pi}{L}n$ .

La frecuencia angular viene dada por:

$LaTeX: \omega_n= k_nv$

Donde $LaTeX: n=1,2,3,....$ , y $LaTeX: v$ es la velocidad de fase.

Procedimiento Experimental

Para ambos casos (ondas transversales y longitudinales) se usa el siguiente equipamiento:

- Generador de funciones.

- Parlante.

Determinación de las masas

- Mida la masa de la cuerda utilizando la balanza PL202-s

- Mida las masas utilizando la balanza PL3001-s

- Utilice los manuales de las balanzas para poder determinar errores sistematicos. En ellos podra encontrar información como se muestra a continuación:

 Balanza: PL 3001-s

 * Precisión minima: 0.1  gr
 * Repetición:       0.08 gr
 * linealidad:       0.2  gr

                    0.4  gr

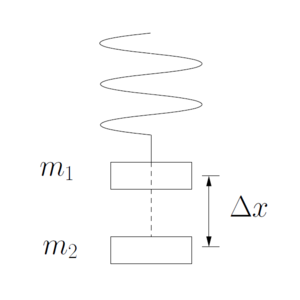
Determinación de la constante elástica del resorte

Ondas Transversales

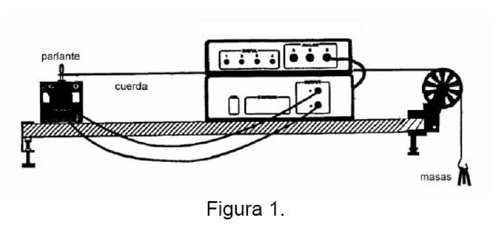
1. Las ondas son generadas en una cuerda excitada transversalmente por un parlante vibrando a frecuencia variable, como muestra la figura 1. La cuerda está unida por un extremo al centro del parlante, y en el otro extremo tiene un gancho para agregar masas, generando una tensión variable en el extremo libre.

2. La tensión de la cuerda se ajusta agregando golillas al gancho del extremo colgante. La tensión de la cuerda debe ser baja.

3. Mida la densidad lineal de masa de la cuerda.

4. Conecte el parlante al amplificador de potencia.

5. Para distintos valores de la tensión de la cuerda, encuentre las frecuencias correspondientes a los modos normales de vibración, caracterizados por el número $LaTeX: n$ correspondiente.

6. Usando gráficos de la forma $LaTeX: \omega$ $LaTeX: versus$ $LaTeX: n$ , determine para las distintas tensiones la velocidad de propagación de ondas transversales en la cuerda.

7. Analice gráficamente la relación entre la tensión de la cuerda y la velocidad de propagación de las ondas.

Ondas Longitudinales

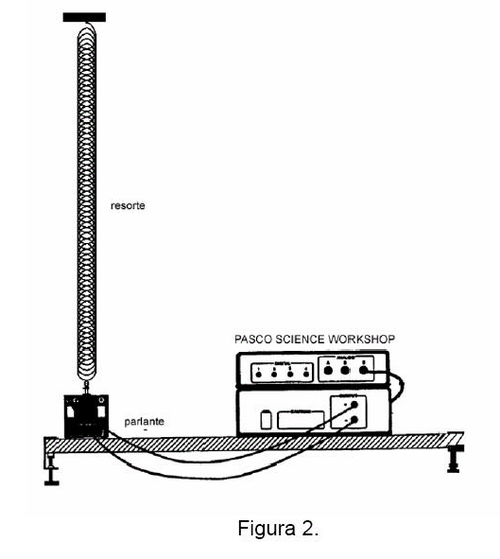
1. Las ondas son generadas en un resorte excitado longitudinalmente por un parlante vibrando a frecuencia variable, como muestra la figura 2. El resorte está unido por un extremo al centro del parlante y el otro extremo está fijo. La tensión del resorte se ajusta variando su largo extendido. Al igual que en el caso anterior la tensión del resorte debe ser baja.

2. Determine la constante elástica del resorte.

3. Para distintos valores de la tensión del resorte, encuentre las frecuencias correspondientes a los modos normales de vibración, caracterizados por el número $LaTeX: n$ correspondiente.

4. Usando gráficos de la forma $LaTeX: \omega$ $LaTeX: versus$ $LaTeX: n$ , determine para las distintas tensiones la velocidad de propagación de ondas longitudinales en el resorte.

5. Analice gráficamente la relación entre la tensión del resorte y la velocidad de propagación de las ondas.

Revision as of 15:26, 15 July 2013 (view source) Sugodoy (Talk \| contribs) (→‎Ondas Transversales) ← Older edit		Revision as of 15:27, 15 July 2013 (view source) Sugodoy (Talk \| contribs) (→‎Ondas Transversales) Newer edit →
Line 63:		Line 63:


−	[[File:Ac3.png\|center\|thumb\|500px\|]]	+	[[File:AC3.png\|center\|thumb\|500px\|]]

	: 5. Para distintos valores de la tensión de la cuerda, encuentre las frecuencias correspondientes a los modos normales de vibración, caracterizados por el número <math>n</math> correspondiente.		: 5. Para distintos valores de la tensión de la cuerda, encuentre las frecuencias correspondientes a los modos normales de vibración, caracterizados por el número <math>n</math> correspondiente.

Ondas Estacionarias en 1-D (Fiz0312)

Revision as of 15:27, 15 July 2013

Contents