Ondas Estacionarias de Sonido (Fiz0312)

Revision as of 15:08, 6 March 2013

Ondas Estacionarias de Sonido

Objetivo

El experimento base consiste en el estudio de ondas estacionarias de sonido en un tubo.

La amplitud local de oscilación de las moléculas de aire en el interior de un tubo de largo L en el cuál existen ondas estacionarias de sonido, está descrita por la expresión:

En el caso de un tubo con ambos extremos abiertos, que corresponde a una situación en que las moléculas de aire pueden oscilar longitudinalmente con máxima amplitud en ambos extremos, la condición de amplitud de oscilación máxima en ambos extremos del tubo tiene como consecuencia que las longitudes de onda correspondientes a ondas estacionarias de sonido en el tubo satisfacen la condición

con

Para el caso en que el tubo tenga un extremo cerrado, la condición de amplitud cero de oscilación de las moléculas de aire en el extremo cerrado, implica que las longitudes de onda correspondientes a ondas estacionarias satisfacen la relación:

La longitud de onda y la frecuencia correspondiente se relacionan a través de la ecuación

Donde es la velocidad del sonido, que en el caso de un gas está dada por la expresión:

Siendo el índice adiabático, la constante de Boltzmann, el número de Avogadro, la temperatura y la masa molecular.

Cuando existe una condición de onda estacionaria en el interior del tubo, la onda acústica entra en resonancia, lo que se detecta como un máximo en la amplitud.

Montaje Experimental

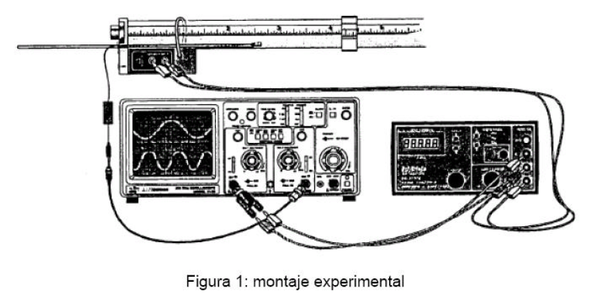
En el experimento se usa un tubo acrílico, que posee un parlante en uno de sus extremos, que actúa como generador de onda de sonido. En las cercanías del parlante, se ubica un micrófono pequeño que permite monitorear la onda acústica en el interior del tubo, desplegando una señal en la pantalla del osciloscopio. Con el osciloscopio se pueden medir tanto la frecuencia como la amplitud de la onda acústica.

Es importante considerar que el micrófono es un transductor de presión, por lo que la amplitud de la señal de medida corresponde a la variación local de presión que experimenta el aire ante la propagación de la onda acústica. La figura 1 muestra un esquema del montaje experimental, que incluye el tubo, con el parlante y su generador de señal, micrófono y osciloscopio.

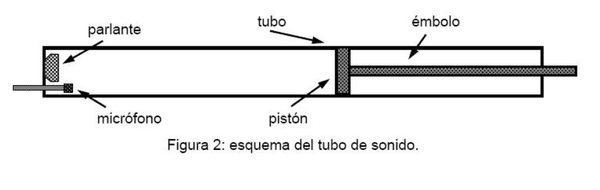
La figura 2 muestra un detalle del tubo. Este tiene en su interior un pistón movil, que permite cambiar el largo efectivo del tubo.

Procedimiento Experimental

1. Conecte el micrófono al osciloscopio y el parlante al generador de señales.

2. Encienda el osciloscopio y seleccione una velocidad de barrido del orden de y una sensibilidad del orden de

3. Encienda el generador de señal y seleccione una frecuencia del orden de .

4. Posicione el postón en la parte central del tubo y ajuste la amplitud de la señal y frecuencia, de modo que se aprecie claramente la señal armónica en la pantalla del osciloscopio. Este ajuste preliminar permite definir el rango operacional de parámetros del experimento.

5. Para distintos valores fijos de la frecuencia, determine las longitudes de tubo correspondientes a ondas estacionarias de sonido en el interior del tubo, identificando, si es posible, el modo correspondiente.

6. Para distintos largos fijos efectivos del tubo, determine las frecuencias correspondientes a ondas estacionarias, identificando, si es posible, el modo correspondiente.

7. Obtenga frecuencias correspondientes a ondas estacionarias para le tubo abierto y cerrado justo en su extremo.

8. A partir de los datos obtenidos, obtenga una medición de velocidad del sonido en el aire en el interior del tubo, y compare el valor obtenido con el que predice la ecuación 5.

9. En el caso de ondas estacionarias obtenidas con el largo total del tubo, con extremo abierto y cerrado compare con lo que predicen las ecuaciones 2 y 3.

10. Discuta y explique posibles variaciones a la forma sinusoidal de la señal acústica que aparecen en determinados rangos de frecuencias o condiciones de resonancia.