Dinámica de Rotación (Fiz 121)

Revision as of 14:32, 15 July 2011

Dinámica de Rotación

Objetivo

Estudiar la dinámica de objetos en movimiento rotacional.

Materiales

- Cámara VideoCom

- Computador con programa VideoCom Movimiento

- Aparato de masas para rotación

- Balanza

- Programa para procesamiento de datos.

Introducción

Las variables dinámicas que describen el proceso de rotación de un objeto sometido a la acción de una fuerza externa son el torque que ejerce la fuerza externa y la aceleración angular resultante de la aplicación del torque.

El torque está dado por la expresión,

$LaTeX: \vec{\tau} = \vec{r} \times \vec{F}$

donde $LaTeX: \vec{F}$ es la fuerza que actúa sobre el objeto y r es el brazo de aplicación de la fuerza, medido desde el eje de rotación.

En estas condiciones, la Segunda Ley de Newton se escribe como

$LaTeX: \vec{\tau} = I\vec{\alpha}$

donde $LaTeX: \alpha$ es la aceleración angular en torno al eje de rotación e $LaTeX: I$ es el momento de inercia del objeto respecto del eje de rotación. La aceleración angular está dada por la expresión,

$LaTeX: \vec{\alpha}=\frac{d^2 \vec{\theta}}{dt^2}=\frac{d\vec{\omega}}{dt}$

donde $LaTeX: \theta$ es el ángulo de rotación, $LaTeX: \omega$ es la velocidad angular y la dirección del vector es la de la normal al plano de rotación.

En forma más general, la Segunda Ley de Newton puede escribirse como

$LaTeX: \vec{\tau}=\frac{d\vec{L}}{dt}$

donde $LaTeX: \vec{L}$ es el momento angular. En este caso tanto $LaTeX: \vec{\tau}$ como $LaTeX: \vec{L}$ están medidos respecto del mismo punto.

El momento angular de una masa puntual respecto de un cierto punto P está dado por la expresión,

$LaTeX: \vec{L}=\vec{r} \times \vec{p}$

donde $LaTeX: \vec{p}$ es el momentum lineal y $LaTeX: \vec{r}$ es el vector posición de la masa respecto de P.

En el caso de un objeto sólido que rota en torno a su eje de simetría con velocidad angular $LaTeX: \omega$ , el momento angular está dado por,

$LaTeX: \vec{L}=I\vec{\omega}$

donde $LaTeX: I$ es el momento de inercia respecto del eje de rotación y el vector apunta a lo largo del eje.

Un objeto puede experimentar rotación en torno a su centro de masa en situación que el centro de masa se encuentra en reposo. En este caso la rotación tiene asociada energía cinética, que está dada por la expresión

$LaTeX: K=\frac{1}{2}I \omega^2$

En un sistema que incluya rotaciones, la ecuación para la energía mecánica del sistema debe incluir tanto los términos de energía potencial, como los de energía cinética de traslación y rotación.

En este laboratorio se estudiará la evolución de las variables dinámicas en procesos de rotación de objetos con simetría cilíndrica, en que el eje de rotación coincide con el eje de simetría

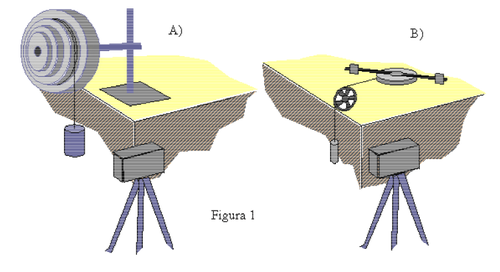
Montaje Experimental

Figura 1: Montaje del del experimento.

Procedimiento

En este laboratorio se desarrollarán dos experimentos:

1. Dinámica de rotación en el plano vertical

2. Dinámica de rotación en el plano horizontal.

En ambos casos el sistema está compuesto por dos masas, una que se mueve en la dirección de la vertical y que al moverse desenrolla una cuerda que hace girar la otra en torno a su eje de simetría. Para el procesamiento cuantitativo de sus datos experimentales necesario conocer la masa de ambos objetos y las dimensiones físicas de los que experimentan movimiento rotatorio.

Montaje A)

a) Para un valor dado de la masa del objeto que se mueve a lo largo de la vertical, registre su movimiento a medida que desenrolla la cuerda y hace que el cuerpo formado por discos concéntricos de radio decreciente efectúe un movimiento rotatorio en el plano vertical. Manteniendo fija la masa que se mueve a lo largo de la vertical, repita la medición enrollando la cuerda en cada uno de los discos.

b )Enrollando la cuerda en uno de los discos, registre el movimiento del objeto a lo largo de la vertical, repitiendo para distintos valores de la masa de éste.

Montaje B)

a) Para un valor dado de la masa del objeto que se mueve a lo largo de la vertical, registre su movimiento a medida que desenrolla la cuerda y hace que la barra vertical efectúe un movimiento rotatorio en el plano horizontal. Manteniendo fija la masa que se mueve a lo largo de la vertical, repita la medición para distintas posiciones de las masas ubicadas sobre la barra. En estas mediciones es importante cuidar que las masas ubicadas a ambos lados de la barra se encuentren a la misma distancia del centro de la misma.

b) Fijando la posición radial de las masas sobre la barra, registre el movimiento del objeto a lo largo de la vertical, repitiendo para distintos valores de la masa de éste.

Análisis

Determine experimentalmente el momento de inercia del cuerpo formado por los discos superpuestos.

Encuentre el momento de inercia de la barra, para las distintas posiciones radiales de las masas consideradas en sus mediciones.

En ambos casos anteriores compare su medición con el valor para el momento de inercia respectivo calculado teóricamente.

Genere gráficos que muestren en sus experimentos la evolución temporal del momento angular total del sistema.

A partir de los gráficos obtenidos, discuta la conservación del momento angular en sus sistema.

@@ Line 27: / Line 27: @@
-:<math>\vec{\tau} = \vec{r} \times \vec{F}</math>
+:::<math>\vec{\tau} = \vec{r} \times \vec{F}</math>
 donde <math>\vec{F}</math> es la fuerza que actúa sobre el objeto y r es el brazo de aplicación de la fuerza, medido desde el eje de rotación.
@@ Line 33: / Line 33: @@
 En estas condiciones, la Segunda Ley de Newton se escribe como
-<math>\vec{\tau} = I\vec{\alpha}</math>
+:::<math>\vec{\tau} = I\vec{\alpha}</math>
 donde <math>\alpha</math> es la aceleración angular en torno al eje de rotación e <math>I</math> es el momento de inercia del objeto respecto del eje de rotación. La aceleración angular está dada por la expresión,
-:<math>\vec{\alpha}=\frac{d^2 \vec{\theta}}{dt^2}=\frac{d\vec{\omega}}{dt}</math>
+:::<math>\vec{\alpha}=\frac{d^2 \vec{\theta}}{dt^2}=\frac{d\vec{\omega}}{dt}</math>
@@ Line 44: / Line 44: @@
 En forma más general, la Segunda Ley de Newton puede escribirse como
-:<math>\vec{\tau}=\frac{d\vec{L}}{dt}</math>
+:::<math>\vec{\tau}=\frac{d\vec{L}}{dt}</math>
@@ Line 57: / Line 57: @@
 En el caso de un objeto sólido que rota en torno a su eje de simetría con velocidad angular <math>\omega</math>, el momento angular está dado por,
-:<math>\vec{L}=I\vec{\omega}</math>
+:::<math>\vec{L}=I\vec{\omega}</math>
 donde <math>I</math> es el momento de inercia respecto del eje de rotación y el vector apunta a lo largo del eje.
@@ Line 63: / Line 63: @@
 Un objeto puede experimentar rotación en torno a su centro de masa en situación que el centro de masa se encuentra en reposo. En este caso la rotación tiene asociada energía cinética, que está dada por la expresión
-:<math>K=\frac{1}{2}I \omega^2</math>
+:::<math>K=\frac{1}{2}I \omega^2</math>
 En un sistema que incluya rotaciones, la ecuación para la energía mecánica del sistema debe incluir tanto los términos de energía potencial, como los de energía cinética de traslación y rotación.

Dinámica de Rotación (Fiz 121)

Revision as of 14:32, 15 July 2011

Contents