Fuerza Centrípeta (Fis1510 DS)

Revision as of 16:15, 3 July 2011

Fuerza Centrípeta

Objetivo

Estudiar experimentalmente la 2a ley de Newton (Ley de masa) para el caso de un movimiento circular uniforme.

Materiales

- Tubo de vidrio

- Tapón de goma

- Golillas

- Trozo de hilo

- Un clip

- Gancho de alambre

- Cronómetro

- Balanza

- Huincha de medir

Introducción

En esta sección se pretende fijar su atención en algunos conceptos, criterios, etc., a fin de que la realización de su experiencia sea hecha de un modo natural y lógico y no automáticamente. Por este motivo se proponen algunas actividades que Ud. deberá realizar. Como Ud. sabe, un movimiento periódico es aquel que se repite cada cierto intervalo de tiempo, que llamaremos periodo ( $LaTeX: T$ ). En nuestro experimento el Periodo se expresará como:

$LaTeX: T=\frac{t}{\mbox{numero de revoluciones}}$

donde $LaTeX: t$ es el tiempo empleado en efectuarse cierto número de revoluciones. Otro parámetro a considerar dentro del movimiento rotacional es el de Velocidad angular ( $LaTeX: \omega$ ). Este se define como:

$LaTeX: \omega = \frac{2 \pi}{T}$

Procedimiento

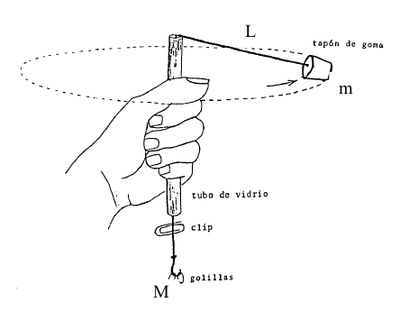
1) Arme el sistema de la figura 1.

2) Mida los siguientes parámetros:

a) masa del tapón : (m)

b) la longitud entre el tapón y el tubo: (L).

3) El clip que se coloca sobre el hilo en la parte inferior del tubo sirve de indicador para mantener constante el largo del tramo de hilo que va desde el tapón hasta el borde del tubo.

4) Cargue el gancho con un número apropiado de golillas de tal modo que las rotaciones permitan realizar la medición con facilidad. Registre la masa de las golillas mas la masa del gancho empleado.(M = masa golillas+masa gancho). Sostenga el tubo en posición vertical, moviéndolo un poco circularmente para producir y mantener el movimiento del tapón de goma en una órbita circular horizontal de modo que la velocidad angular sea constante. (ver figura 1).

Figura 1: Disposición de los materiales.

5) Mida con el cronómetro el tiempo transcurrido en efectuarse 10 revoluciones a la máxima velocidad rotacional que permita mantener el clip a distancia fija del tubo, y después mida el tiempo a la mínima velocidad rotacional. (La diferencia entre estos tiempos se debe principalmente al roce entre el hilo y el tubo). Registre los valores del tiempo medidos en esta experiencia.

6) Repita los pasos anteriores para 5 mediciones diferentes de la Tensión.(Para variar la tensión del hilo cambie el número de golillas a colgar).

7) La velocidad de rotación debe ajustarse de modo que el clip se mantenga cerca del tubo, pero sin tocarlo. La velocidad de rotación del tapón se puede variar en un rango amplio sin que el clip se deslice.

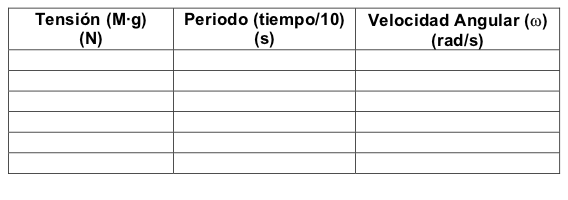
8) Resuma sus datos en una tabla como la siguiente.

Tabla 1 Longitud Constante _____________ mts

Tabla 1

Figura 2: Diagrama de Fuerzas.

9) Repita el procedimiento anterior, pero esta vez mantenga constante la Tensión y varíe la longitud de la cuerda, para unas cinco mediciones diferentes.

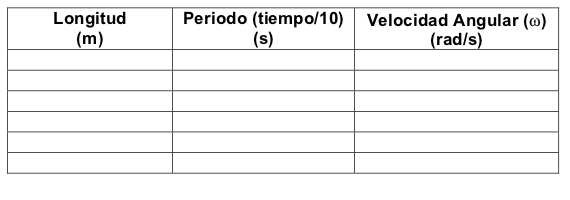
10) Resuma sus datos en una tabla como la tabla 2.

Tabla 2 Tensión Constante _____________ N

Tabla 2

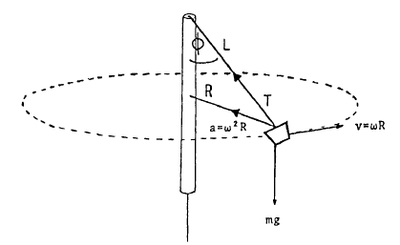
A partir del diagrama de fuerzas de la figura 2, podemos deducir la ecuación que representa la 2a Ley de Newton para éste experimento:

$LaTeX: T=m \omega^2 L$

(ver demostración en Halliday-Resnik)

Análisis

Grafique en un papel milimetrado Tensión vs $LaTeX: \omega ^2$ .
Escriba la ecuación que representa la curva graficada.
¿Con que expresión matemática puede relacionar la ecuación obtenida?.
Obtenga el valor de la pendiente con sus unidades respectivas (S.I.) e interprete físicamente éste valor. Obtenga el porcentaje de error.
Con sus resultados ¿cree Ud. que se comprueba la 2a Ley de Newton para éste movimiento rotacional?.Explique .
Grafique en un papel milimetrado Longitud vs $LaTeX: 1/ \omega^2$
Escriba la ecuación que representa la curva graficada en (6.).
¿Con que expresión matemática puede relacionar la ecuación obtenida en el punto (7.)?
Obtenga el valor de la pendiente con sus unidades respectivas (S.I.) e interprete físicamente éste valor. Obtenga el porcentaje de error.
¿Cuál de éstos dos métodos se acercó mas al valor teórico que le permitió comprobar la Segunda Ley de Newton?.

@@ Line 33: / Line 33: @@
 Como Ud. sabe, un movimiento periódico es aquel que se repite cada cierto intervalo de tiempo, que llamaremos '''periodo''' (<math>T</math>). En nuestro experimento el Periodo se expresará como:
-:<math>T=\frac{t}{\mbox{numero de revoluciones}}</math>
+:<center><math>T=\frac{t}{\mbox{numero de revoluciones}}</math></center>
 donde <math>t</math> es el tiempo empleado en efectuarse cierto número de revoluciones.
 Otro parámetro a considerar dentro del movimiento rotacional es el de '''Velocidad angular''' (<math>\omega</math>). Este se define como:
-:<math>\omega = \frac{2 \pi}{T}</math>
+:<center><math>\omega = \frac{2 \pi}{T}</math></center>
 === Procedimiento ===

Fuerza Centrípeta (Fis1510 DS)

Revision as of 16:15, 3 July 2011

Contents