Sistemas de Poleas (Fis 151/Fis 1513)
(→Procedimiento) |
|||
| Line 53: | Line 53: | ||
| − | 4.-Desplace un colgante una cierta distancia, mídala (<math>h_1</math>). Mida el desplazamiento del otro colgante (<math>h_2</math>) con respecto al punto inicial. |
+ | 4.-Desplace un colgante una cierta distancia, mídala (<m>h_1</m>). Mida el desplazamiento del otro colgante (<m>h_2</m>) con respecto al punto inicial. |
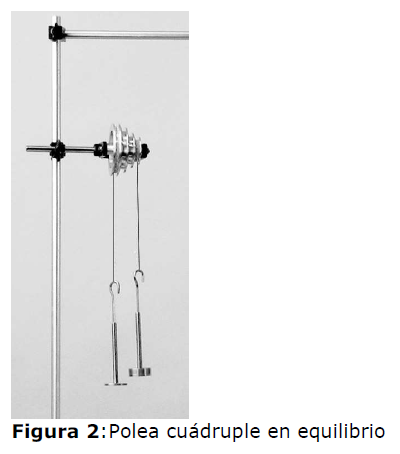
5.- Cuelgue masas en ambos colgantes hasta dejar el sistema en equilibrio. Anote el valor de estas masas (Figura 2) para 2 configuraciones distintas. |
5.- Cuelgue masas en ambos colgantes hasta dejar el sistema en equilibrio. Anote el valor de estas masas (Figura 2) para 2 configuraciones distintas. |
||
| Line 100: | Line 100: | ||
- cuerda |
- cuerda |
||
| − | - Sensor de Fuerza, <math>50 N</math> (''Pasco'') |
+ | - Sensor de Fuerza, <m>50 N</m> (''Pasco'') |
| − | - 1 Dinamómetro de 10 N<math>Escribir la fórmula aquí</math> |
+ | - 1 Dinamómetro de 10 N<m>Escribir la fórmula aquí</m> |
| − | - Masa de <math>500 gr</math>. |
+ | - Masa de <m>500 gr</m>. |
- Balanza digital |
- Balanza digital |
||
| Line 125: | Line 125: | ||
| − | 3.- En el otro extremo de la cuerda ate un dinamómetro de <math>10 N</math>, el cual medirá la fuerza externa aplicada al sistema. (ver figura 6) |
+ | 3.- En el otro extremo de la cuerda ate un dinamómetro de <m>10 N</m>, el cual medirá la fuerza externa aplicada al sistema. (ver figura 6) |
[[File:Pol6.png|center|thumb|500px| ]] |
[[File:Pol6.png|center|thumb|500px| ]] |
||
| Line 143: | Line 143: | ||
: 1.- En el mismo programa, obtenga el gráfico Fuerza sensor vs fuerza dinamómetro. Interprete físicamente el valor de la pendiente. |
: 1.- En el mismo programa, obtenga el gráfico Fuerza sensor vs fuerza dinamómetro. Interprete físicamente el valor de la pendiente. |
||
| − | : 2.- Reemplace el sensor de Fuerza por una masa de <math>500 gr</math>. En base al punto anterior calcule la masa que se necesita para levantar los 500 gr. |
+ | : 2.- Reemplace el sensor de Fuerza por una masa de <m>500 gr</m>. En base al punto anterior calcule la masa que se necesita para levantar los 500 gr. |
: 3.-¿Puede encontrar alguna relación entre la fuerza aplicada y el numero de poleas que conforman el polipasto para levantar una cierta masa? |
: 3.-¿Puede encontrar alguna relación entre la fuerza aplicada y el numero de poleas que conforman el polipasto para levantar una cierta masa? |
||
| Line 152: | Line 152: | ||
| − | ==Experimento III: “ Cálculo de <math>g</math>”== |
+ | ==Experimento III: “ Cálculo de <m>g</m>”== |
| Line 162: | Line 162: | ||
===Introducción=== |
===Introducción=== |
||
| − | En esta experiencia se utilizará una polea de dos pasos, la cual conforma el Sensor de movimiento Rotacional, con el cual se procederá a variar la masa del sistema y medir las variables del movimiento rotacional que permitirá comprobar el valor de <math>g</math>. |
+ | En esta experiencia se utilizará una polea de dos pasos, la cual conforma el Sensor de movimiento Rotacional, con el cual se procederá a variar la masa del sistema y medir las variables del movimiento rotacional que permitirá comprobar el valor de <m>g</m>. |
| Line 171: | Line 171: | ||
| − | <center><math>R_1 \cdot T_1 - R_2 \cdot T_2 = I \cdot \alpha</math></center> |
+ | <center><m>R_1 \cdot T_1 - R_2 \cdot T_2 = I \cdot \alpha</m></center> |
| Line 177: | Line 177: | ||
| − | <center><math>I = M \cdot R_1^2 + M \cdot R_2 ^2</math></center> |
+ | <center><m>I = M \cdot R_1^2 + M \cdot R_2 ^2</m></center> |
| − | siendo <math>M</math> la masa de las poleas, y considerándola despreciable (<math>M \approx 0</math>) |
+ | siendo <m>M</m> la masa de las poleas, y considerándola despreciable (<m>M \approx 0</m>) |
Luego |
Luego |
||
| − | <center><math>R_1 \cdot T_1 = R_2 \cdot T_2</math></center> |
+ | <center><m>R_1 \cdot T_1 = R_2 \cdot T_2</m></center> |
| − | <center><math>\Rightarrow \frac{R_1}{R_2} = \frac{T_2}{T_1} \qquad \qquad \qquad (1)</math></center> |
+ | <center><m>\Rightarrow \frac{R_1}{R_2} = \frac{T_2}{T_1} \qquad \qquad \qquad (1)</m></center> |
| Line 193: | Line 193: | ||
| − | <center><math>m_1 \cdot g - T_1 = m_1 \cdot a_1 \qquad \qquad \qquad (2)</math></center> |
+ | <center><m>m_1 \cdot g - T_1 = m_1 \cdot a_1 \qquad \qquad \qquad (2)</m></center> |
| − | <center><math>m_2 \cdot g - T_2 = m_2 \cdot a_2 \qquad \qquad \qquad (3)</math></center> |
+ | <center><m>m_2 \cdot g - T_2 = m_2 \cdot a_2 \qquad \qquad \qquad (3)</m></center> |
| Line 202: | Line 202: | ||
| − | <center><math>a_2 = - a_1 \frac{R_2}{R_1} </math></center> |
+ | <center><m>a_2 = - a_1 \frac{R_2}{R_1} </m></center> |
| − | <center><math>m_2 \cdot g - \frac{R_1}{R_2} \cdot T_1 = m_2 \cdot \left( - a_1 \cdot \frac{R_2}{R_1} \right) \qquad \qquad \qquad (4)</math></center> |
+ | <center><m>m_2 \cdot g - \frac{R_1}{R_2} \cdot T_1 = m_2 \cdot \left( - a_1 \cdot \frac{R_2}{R_1} \right) \qquad \qquad \qquad (4)</m></center> |
| − | donde <math>a_1=R_1 \alpha</math>. Despejando <math>\alpha</math>, se obtiene |
+ | donde <m>a_1=R_1 \alpha</m>. Despejando <m>\alpha</m>, se obtiene |
| − | <center><math>\alpha = \frac{g \cdot (m_1 \cdot R_1 - m_2 \cdot R_2)}{m_1 \cdot R_1^2 + m_2 \cdot R_2^2} </math></center> |
+ | <center><m>\alpha = \frac{g \cdot (m_1 \cdot R_1 - m_2 \cdot R_2)}{m_1 \cdot R_1^2 + m_2 \cdot R_2^2} </m></center> |
| Line 238: | Line 238: | ||
: 3.- Cuando amarre los hilos en las poleas, asegúrese que los nudos queden por detrás de ésta, para no trancar el movimiento. |
: 3.- Cuando amarre los hilos en las poleas, asegúrese que los nudos queden por detrás de ésta, para no trancar el movimiento. |
||
| − | : 4.- En el programa ''Data Studio'' seleccione el sensor rotacional. En el mismo icono de este sensor seleccione la medición que realizará el sensor, rapidez angular y la frecuencia de muestreo, <math>10 Hz</math>. |
+ | : 4.- En el programa ''Data Studio'' seleccione el sensor rotacional. En el mismo icono de este sensor seleccione la medición que realizará el sensor, rapidez angular y la frecuencia de muestreo, <m>10 Hz</m>. |
| Line 254: | Line 254: | ||
| − | 8.- Usando Excel, realice una gráfica de las aceleraciones angulares obtenidas en el punto <math>7</math> ''versus'' <math>\frac{m_1 R_1 - m_2 R_2}{m_1 R_1^2 + m_2 R_2^2}</math> . Interprete físicamente el valor de la pendiente obtenida. |
+ | 8.- Usando Excel, realice una gráfica de las aceleraciones angulares obtenidas en el punto <m>7</m> ''versus'' <m>\frac{m_1 R_1 - m_2 R_2}{m_1 R_1^2 + m_2 R_2^2}</m> . Interprete físicamente el valor de la pendiente obtenida. |
Revision as of 06:29, 29 October 2014
Contents |
Sistemas de Poleas
Objetivo
Estudiar y aplicar el funcionamiento de un sistema de poleas.
Introducción
La variedad de aplicaciones que presenta el funcionamiento de los sistemas de maquinas simples y compuestas conduce a lo importante que es descubrir y conocer sus principios de funcionamiento y de este modo ampliar el rol que cumple la física en este y otros campos de la ciencia y la tecnología.
En estas experiencias se utilizarán diversos tipos de poleas. Estas se utilizan normalmente para cambiar la dirección de las fuerzas, siendo más fácil levantar la carga.
Experimento I: “Estudio de Reducción en un sistema de Poleas”
Objetivo:
Analizar y comprender intuitivamente la relación existenteentre las diversas variables físico-matemáticas presentes en un sistema de poleas.
Materiales
- Polea 4 pasos
- 2 trozos de cuerdas
- 2 ganchos con pesas
- Balanza digital
- Sistema base para colgar poleas
Procedimiento
- 1.- Arme el sistema que indica la figura 0, utilizando una polea 4 pasos. Pegar una huincha en la varilla izquierda del sistema.
2.- Arme 2 colgantes con pesas, y luego máselos en una balanza digital.
3.- Escoja dos poleas a utilizar. Con un pie de metro mida sus diámetros. Enrolle las cuerdas, en sentido contrario una con respecto a la otra, en cada una de ellas (figura 1).
4.-Desplace un colgante una cierta distancia, mídala (). Mida el desplazamiento del otro colgante (
) con respecto al punto inicial.
5.- Cuelgue masas en ambos colgantes hasta dejar el sistema en equilibrio. Anote el valor de estas masas (Figura 2) para 2 configuraciones distintas.
Análisis
- 1.- A partir de la experiencia realizada con la polea 4 pasos y con los datos obtenidos, encuentre la razón entre los radios de las poleas utilizadas.
2.- Encuentre la razón entre los desplazamientos.
3.- Cuando el sistema se encuentra en equilibrio, encuentre la relación entre las masas colgantes. Compare esta relación con la de los radios y la de los desplazamientos.
- 4.- A partir de los estudios realizados en los puntos anteriores del análisis. ¿Cuál es la interpretación física que Ud. le daría a las relaciones obtenidas de este sistema de poleas?. Fundamente.
Experimento II: “El Polipasto”
Objetivo:
Analizar y comprender intuitivamente la relación existente entre las diversas variables físico-matemáticas presentes en un sistema de poleas.
Introducción
En esta experiencia se utilizará un polipasto, que es un sistema formado por poleas fijas y poleas móviles, las cuales están distribuidas y sujetas a través de cuerdas, el cual se usa para levantar una masa determinada, pero realizando un esfuerzo menor. El polipasto es una combinación de poleas fijas y móviles recorridas por una sola cuerda que tiene uno de sus extremos anclado a un punto fijo.
- Los elementos de este sistema son los siguientes:
La polea fija tiene la función de modificar la dirección de la fuerza externa a ejercer sobre la cuerda. La polea móvil tiene la función de proporcionar ganancia mecánica al sistema. La cuerda transmite las fuerzas entre los diferentes elementos. Su resistencia a la tracción ha de estar en función del valor de la resistencia y de la ganancia mecánica del sistema, que a su vez depende del número de poleas móviles y de su combinación con las fijas.
Materiales
- Polipasto de 6 poleas
- cuerda
- Sensor de Fuerza, (Pasco)
- 1 Dinamómetro de 10 N
- Masa de .
- Balanza digital
- Sistema base para colgar poleas
- Computador con programa Data Studio.
Procedimiento
- 1.- Arme el polipasto tal como aparece en la figura 3.
- 2.- Conecte en la parte inferior del sistema el sensor de fuerza Pasco.(ver figura 5)
3.- En el otro extremo de la cuerda ate un dinamómetro de , el cual medirá la fuerza externa aplicada al sistema. (ver figura 6)
4.- Encienda el computador y ejecute el programa Data Studio. Seleccione el Sensor de Fuerza.
5.- En el menú del programa, selecciones Opciones y active la opción de ingresar información por teclado. En este caso Ud. ingresará el valor que indica el dinamómetro.
6.- Una vez ajustado bien el dinamómetro al polipasto, comience a aumentar la fuerza externa (de a 1 N), registre el valor entregado por el dinamómetro seleccionando en el programa Keep e ingrese los valores a medida que vaya aumentando la fuerza.
Análisis
- 1.- En el mismo programa, obtenga el gráfico Fuerza sensor vs fuerza dinamómetro. Interprete físicamente el valor de la pendiente.
- 2.- Reemplace el sensor de Fuerza por una masa de
. En base al punto anterior calcule la masa que se necesita para levantar los 500 gr.
- 3.-¿Puede encontrar alguna relación entre la fuerza aplicada y el numero de poleas que conforman el polipasto para levantar una cierta masa?
- Encuentre el error experimental con respecto al teórico.
Experimento III: “ Cálculo de  ”
”
Objetivo
Obtener el valor de la aceleración de gravedad utilizando un sistema de poleas.
Introducción
En esta experiencia se utilizará una polea de dos pasos, la cual conforma el Sensor de movimiento Rotacional, con el cual se procederá a variar la masa del sistema y medir las variables del movimiento rotacional que permitirá comprobar el valor de .
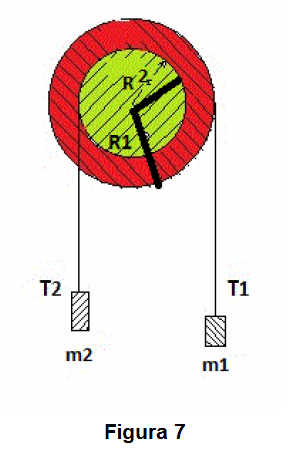
De la figura 7 se obtiene la ecuación del movimiento para el sistema:
donde,
siendo la masa de las poleas, y considerándola despreciable (
)
Luego
Para este sistema se tiene las siguientes ecuaciones de fuerzas:
Reemplazando (1) en (3), y considerando la restricción cinemática:
donde . Despejando
, se obtiene
Materiales
- Sensor de Movimiento Rotacional Pasco
- 2 trozos de hilo
- 2 ganchos con masas
- Balanza digital
- Sistema base para colgar poleas
- Computador con programa Data Studio.
Procedimiento
- 1.- Instale el Sensor de movimiento rotacional en la base metálica, y conéctelo a la interfaz. Asegúrese que el cable amarillo esté en el Canal A y el cable negro en el Canal B.
- 2.- Cuelgue los hilos en las poleas del sensor con las pesas y sus ganchos previamente masadas en la balanza. Ver Figura 8.
- 3.- Cuando amarre los hilos en las poleas, asegúrese que los nudos queden por detrás de ésta, para no trancar el movimiento.
- 4.- En el programa Data Studio seleccione el sensor rotacional. En el mismo icono de este sensor seleccione la medición que realizará el sensor, rapidez angular y la frecuencia de muestreo,
.
- 5.- En el programa presione Start, y en ese momento suelta el sistema, presione Stop cuando las pesas hayan terminado su recorrido.
- 6.- Obtenga el gráfico rapidez angular vs tiempo. Observe la curva obtenida y encuentre el mejor valor para la pendiente del gráfico. Para ello realice un ajuste lineal (incorporado en el programa).
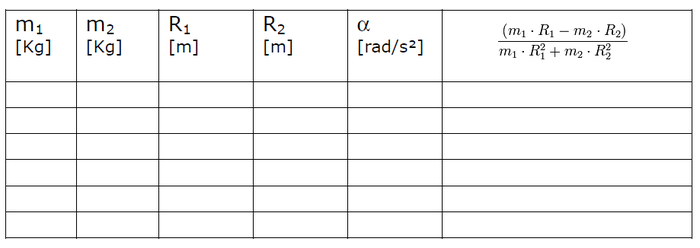
- 7.- Realice la experiencia nuevamente para 5 pares diferentes de masas colgantes. Repita el punto 6 para cada experiencia. Realice una tabla como la siguiente:
8.- Usando Excel, realice una gráfica de las aceleraciones angulares obtenidas en el punto versus
. Interprete físicamente el valor de la pendiente obtenida.