Interferencia y Difracción (Fiz0312)
(→Objetivo) |
|||
| Line 16: | Line 16: | ||
Cuando un haz de luz monocromática y paralela, por ejemplo, un haz de laser, de longitud de onda <math>\lambda</math> incide sobre una ranura angosta de ancho <math>a</math>, como muestra la figura 1, la distribución de intensidad sobre una pantalla ubicada a distancia <math>D</math> está dada por la expresión: |
Cuando un haz de luz monocromática y paralela, por ejemplo, un haz de laser, de longitud de onda <math>\lambda</math> incide sobre una ranura angosta de ancho <math>a</math>, como muestra la figura 1, la distribución de intensidad sobre una pantalla ubicada a distancia <math>D</math> está dada por la expresión: |
||
| − | :<center><math>I(\alpha)=I_0 \frac{\sin^2(\beta)}{\beta^2}</math> (1) </center> |
+ | :<center><math>I(\alpha)=I_0 \frac{\sin^2(\beta)}{\beta^2} \qquad\qquad\qquad (1)</math> </center> |
donde, |
donde, |
||
| − | :<center><math>\beta=\frac{\pi a}{\lambda}\cdot \sin(\theta)</math> (2) </center> |
+ | :<center><math>\beta=\frac{\pi a}{\lambda}\cdot \sin(\theta) \qquad\qquad\qquad (2)</math> </center> |
y, |
y, |
||
| − | :<center><math>\sin(\theta)=\frac{D^2}{y^2+D^2}</math> (3) </center> |
+ | :<center><math>\sin(\theta)=\frac{D^2}{y^2+D^2} \qquad\qquad\qquad (3)</math> </center> |
| Line 30: | Line 30: | ||
| − | :<center><math>I(\theta)=4I_0 \cdot \frac{\sin^2(\beta)}{\beta^2} \cdot \cos^2(\alpha)</math> (4) </center> |
+ | :<center><math>I(\theta)=4I_0 \cdot \frac{\sin^2(\beta)}{\beta^2} \cdot \cos^2(\alpha) \qquad\qquad\qquad (4)</math> </center> |
donde, |
donde, |
||
| − | :<center><math>\alpha=\frac{\pi d}{\lambda} \cdot \sin(\theta)</math> (5) </center> |
+ | :<center><math>\alpha=\frac{\pi d}{\lambda} \cdot \sin(\theta) \qquad\qquad\qquad (5)</math> </center> |
y <math>\beta</math> y <math>\theta</math> están definidos por las ecuaciones (2) y (3) respectivamente. |
y <math>\beta</math> y <math>\theta</math> están definidos por las ecuaciones (2) y (3) respectivamente. |
||
Revision as of 14:10, 15 July 2011
Contents |
Interferencia y Difracción
Objetivo
Estudiar la formación de franjas de interferencia y difracción por ranuras angostas.
Introducción
Al iluminar con un haz de luz monocromático un conjunto de ranuras angostas y paralelas, la luz reflectada por las ranuras interfiere generando un patrón de franjas de irradianza variable, paralelas a las ranuras, en las cuales la distribución de intensidad está determinada por efectos de interferencia y difracción. En el caso en que la distancia entre el plano de observación de las franjas y posición de las ranuras es grande comparada con el tamaño de estas, la distribución de intensidad en las franjas se puede calcular usando la aproximación de Fraunhofer
Cuando un haz de luz monocromática y paralela, por ejemplo, un haz de laser, de longitud de onda incide sobre una ranura angosta de ancho
, como muestra la figura 1, la distribución de intensidad sobre una pantalla ubicada a distancia
está dada por la expresión:
donde,
y,
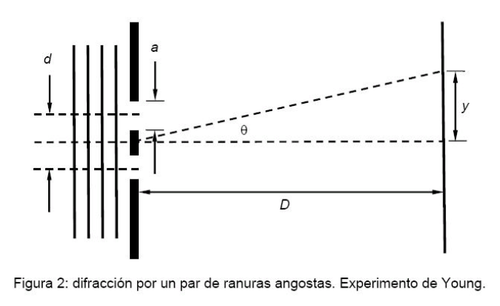
En el experimento de Young dos ranuras paralelas de ancho y separadas una distancia
son iluminadas por un frente plano de luz monocromática de longitud de onda
, como muestra la figura 2. Al observar la distribución de luz sobre una pantalla a distancia
de las ranuras, se observan franjas de interferencia dadas por la relación:
donde,
y y
están definidos por las ecuaciones (2) y (3) respectivamente.
Equipamiento
- Láser ().
- Placa con una ranura o ranura de ancho ajustable.
- Diapositiva con dos ranuras paralelas.
- Camara Videocom, con arreglo de diodos.
- Polarizador.
- Filtro Rojo.
- Regla.
- Microscopio.
- Computador
Procedimiento Experimental
Montaje Básico
- Monte el láser sobre el banco óptico y, luego de encenderlo, alinee el láser con la cámara Videocom apagada, cuidado que el punto de iluminación del láser esté ubicado en el centro de arreglo de diodos de la cámara.
- Ponga el polarizador en frente del láser y el filtro rojo sobre la entrada de la cámara.
- Encuenda la cámara Videocom y póngala en el modo de adquisición de INTENSIDAD.
- Ajuste la posición y gire el polarizador de modo que el máximo haz láser quede dentro de la escala.
Difracción por una Ranura Única
- 1. Mida, usando el microscopio con el ancho de una ranura en particular.
- 2. Coloque la ranura con ancho conocido en el camino del haz de láser, orientada perpendicular al arreglo de diodos.
- 3. Gire el polarizador de modo tal que la distribución de intensidades detectada por el arreglo de diodos quede dentro de la escala del gráfico respectivo. Las franjas de interferencia más finas superpuestas a la distribución con máximo central se deben a interferencia de la luz láser por reflexiones en el recubrimiento transparente sobre los pixel del arreglo de diodos.
- 4. Obtenga mediciones de la distribución de intensidades para al menos tres valores de la distancia entre la ranura y el arreglo de diodos, en el rango
- 5. Usando los valores de ancho de ranura, longitud de onda del láser y distancia ranura-plano de detección, obtenga gráficos teóricos de la distribución de intensidad difractada.
Difracción por Dos Ranuras. Experimento de Young
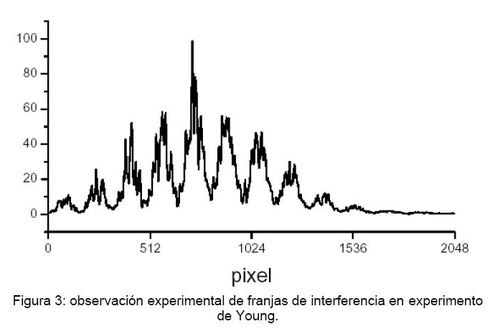
- 1. Coloque una dispositiva con las ranuras en el camino del haz láser, ajuste la posición y gire nuevamente el polarizador, hasta que la distribución de intensidades en la pantalla sea similar a la que muestra la figura 3.
- 2. Las franjas de interferencia más finas superpuestas a las franjas de Young se deben a interferencia de la luz láser por reflexiones en el recubrimiento transparente sobre los pixeles del arreglo de diodos
- 3. Registre un conjunto de datos correspondiente a un diagrama de interferencia.
- 4. Mida la distancia entre las ranuras y el arreglo de diodos, que corresponde a su plano de observación.
- 5. Use el microscopio para medir la separación entre las franjas e intente medir su ancho.
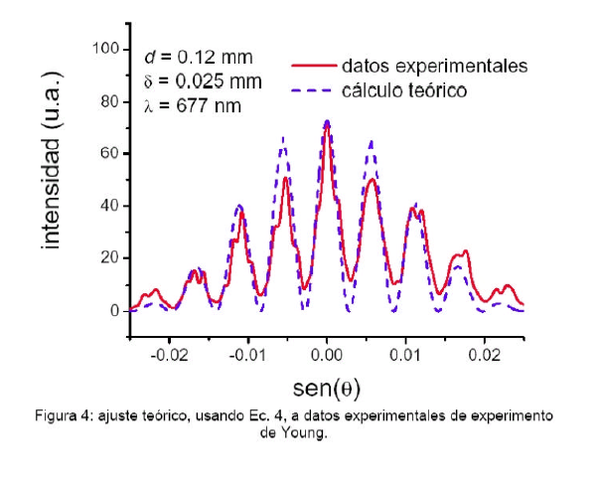
- 6. El primer término de la ecuación (4) corresponde al efecto de difracción y el segundo al de interferencia. Usando su medición de separación entre ranuras, genere un gráfico de franjas de interferencia. Ajuste el valor de la separación entre las ranuras para que los máximos calculados coincidan con los observados.
- 7. Usando un valor medido o uno tentativo (menor que la separación ajustada en e paso anterior) genere un gráfico del término de difracción y ajuste con él el ancho de las ranuras, de modo que corresponda con la modulación de amplitud observada.
- 8. Con los valores ajustados de ancho y separación de ranuras, genere el diagrama teórico de distribución de intensidades y compárelo con el obtenido experimentalmente.
- 9. Discuta sus resultados y los ajustes hechos para reproducir los resultados experimentales.
- 10. Su resultado final debería parecerse al de la figura 4. En este caso, los datos experimentales han sido suavizados para eliminar las franjas finas de interferencia, esto usando un filtro FFT(Fast Fourier Transform) con 25 puntos