Ondas Estacionarias en 1-D (Fiz0312)
(→Introducción) |
Soltorresm (Talk | contribs) (→Ondas Longitudinales) |
||
| (91 intermediate revisions by 5 users not shown) | |||
| Line 5: | Line 5: | ||
Estudiar ondas estacionarias en un medio 1-D |
Estudiar ondas estacionarias en un medio 1-D |
||
| − | |||
=== Introducción=== |
=== Introducción=== |
||
| − | El experimento coniste en el estudio de modos normales de vibración asociados a ondas estacionarias transversales y longitudeinales en un medio 1-D. |
+ | El experimento consiste en el estudio de modos normales de vibración asociados a ondas estacionarias transversales y longitudinales en un medio 1-D. |
| − | Los modos normales de vibración asociados a ondas estacionarias en un medio 1-D de largo L, con extremos fijos, tienen la forma: |
+ | Los modos normales de vibración asociados a ondas estacionarias en un medio 1-D de largo L, con ambos extremos fijos, tienen una elongación de la forma: |
| − | :<center><math>y_n(x,t)=A\sin(k_n x) \cdot \cos(\omega_n t)</math></center> |
+ | :<center><m>y_n(x,t)=A\sin(k_n x) \cdot \sin(\omega_n t + \varphi)</m></center> |
| − | en el caso de ondas transversales, y |
+ | tanto para ondas transversales como para ondas longitudinales, cuyo número de onda viene dado por: |
| − | :<center><math>s_n(x,t)=A\sin(k_n x) \cdot \cos(\omega_n t)</math></center> |
+ | :<m>k_n = \frac{\pi}{L}n</m>. |
| + | La frecuencia angular viene dada por: |
||
| − | Para el caso de ondas longitudinales. |
+ | :<m>\omega_n= k_nv</m> |
| − | En ambos casos, |
+ | Donde <m>n=1,2,3,....</m>, y <m>v</m> es la velocidad de fase. |
| − | :<math>k_n=n \pi /L</math> |
+ | ===Procedimiento Experimental=== |
| − | :<math>\omega_n=n \pi v/L</math> |
+ | Para ambos casos (ondas transversales y longitudinales) se usa el siguiente equipamiento: |
| − | y <math>n=1,2,3,....</math>, y <math>v</math> es la velocidad de propagación de las ondas en el medio. |
+ | - Generador de funciones. |
| − | ===Procedimiento Experimental=== |
+ | - Parlante. |
| − | Para ambos casis, ondas transversales y longitudinales, se usa el siguiente equipamiento: |
+ | == '''Determinación de las masas'''== |
| − | - Amploficador de potencia ''PASCO CI-6502'' |
+ | - Mida la masa de la cuerda utilizando la balanza PL202-s |
| − | - Computador PC con interfaz ''PASCO SCIENCE WORKSHOP'' |
+ | - Mida las masas utilizando la balanza PL3001-s |
| − | - Parlante. |
+ | - Utilice los manuales de las balanzas para poder determinar '''errores sistematicos'''. En ellos podra encontrar información como se muestra a continuación: |
| + | |||
| + | Balanza: PL 3001-s |
||
| − | - Programa ''DATA STUDIO''. |
+ | * Precisión minima: 0.1 gr |
| + | * Repetición: 0.08 gr |
||
| + | * linealidad: 0.2 gr |
||
| + | ------------------------------- |
||
| + | <m>\approx</m> 0.4 gr |
||
| + | == '''Determinación de la constante elástica del resorte'''== |
||
| − | == Ondas Transversales== |
+ | Para determinar la constante elástica coloque una masa en el resorte colgando de uno de sus extremos. Defina la posición de esta masa como origen de sistema de coordenadas o posición de referencia. Luego agregue otra masa al resorte (aumentando la masa) y mida el desplazamiento que se produce con respecto a la posición de referencia, como se muestra en la figura 1. |
| − | : 1. Las ondas son generadas en una cuerda excitada transversalmente por un parlante vibrando a frecuencia variable, como muestra la figura 1. La cuerda está unida por un extremo al centro del parlante, y tiene un gancho para agregar masas, generando una tensión variable en el extremo libre |
+ | Utilizando la ecuación de equilibrio de fuerzas |
| − | : 2. La tensión de la cuerda se ajusta agregando golillas al gancho del extremo colgante. <u>'''No agregue más de 12 golillas al gancho'''</u>. |
+ | :<center><m>(m_f-m_i)g=K\Delta x,</m></center> |
| − | : 3. Mida la densidad lineal de masa de la cuerda. |
+ | Mediante métodos gráficos, considerando las barras de error apropiadas en cada caso, determine la constante del resorte. |
| − | : 4. Conecte el parlante al amplificador de potencia. |
||
| + | [[File:figura1.png|center|thumb|300px|]] |
||
| + | |||
| + | == '''Ondas Transversales'''== |
||
| + | |||
| + | : 1. Las ondas son generadas en una cuerda excitada transversalmente por un parlante vibrando a frecuencia variable, como muestra la figura 2. La cuerda está unida por un extremo al centro del parlante, y en el otro extremo tiene un gancho para agregar masas, generando una tensión variable en el extremo libre. |
||
| + | |||
| + | : 2. La tensión de la cuerda se ajusta agregando golillas al gancho del extremo colgante. La tensión de la cuerda debe ser baja. |
||
| + | |||
| + | : 3. Mida la densidad lineal de masa de la cuerda. |
||
| − | [[File:Ac2.png|center|thumb|500px|]] |
+ | : 4. Conecte el parlante al generador de funciones. |
| + | '''Warning''': El o los botones atenuadores NO deben estar activos. |
||
| − | : 5. Conecte el amplificador de potencia de la interfaz ''PASCO''. |
+ | [[File:figura_2.png|center|thumb|500px|]] |
| − | : 6. Active el programa ''Data Studio''. |
+ | : 5. Para distintos valores de la tensión de la cuerda, encuentre las frecuencias correspondientes a los modos normales de vibración, caracterizados por el número <m>n</m> correspondiente. |
| − | : 7. En el programa seleccione ''Amplificador de Potencia'' y luego forma de onda ''AC Waveform''. Luego de encendido el amplificador de potencia, selecciones <math>5V</math> '''(no más)''' para la amplitud de la señal, y una frecuencia inicial del orden de los <math>20Hz</math>. |
+ | : 6. Usando gráficos de la forma <m>\omega</m> <m>versus</m> <m>n</m>, determine para las distintas tensiones la velocidad de propagación de ondas transversales en la cuerda. |
| − | : 8. Para distintos valores de la tensión de la cuerda, encuentre las frecuencias corrspondientes a los modos normales de vibración, caracterizados por el número <math>n</math> correspondiente. |
+ | : 7. Analice gráficamente la relación entre la tensión de la cuerda y la velocidad de propagación de las ondas. |
| − | : 9. Usando gráficos de la forma <math>\omega</math> <math>versus</math> <math>n</math>, determine para las distintas tensiones la velocidad de propagación de ondas transversales en la cuerda. |
+ | == '''Ondas Longitudinales''' == |
| − | : 10. Analice gráficamente la relación entre la tensión de la cuerda y la velocidad de propagación de las ondas. |
+ | : 1. Las ondas son generadas en un resorte excitado longitudinalmente por un parlante vibrando a frecuencia variable, como muestra la figura 3. El resorte está unido por un extremo al centro del parlante y el otro extremo está fijo. La tensión del resorte se ajusta variando su largo extendido. Al igual que en el caso anterior la tensión del resorte debe ser baja. |
| + | : 2. Para distintos valores de la tensión del resorte, encuentre las frecuencias correspondientes a los modos normales de vibración, caracterizados por el número <m>n</m> correspondiente. |
||
| − | == Ondas Longitudinales == |
+ | : 3. Usando gráficos de la forma <m>\omega</m> <m>versus</m> <m>n</m>, determine para las distintas tensiones la velocidad de propagación de ondas longitudinales en el resorte. |
| − | : 1. Las ondas son generadas en un resorte excitado longitudinalmente por un parlante vibrando a frecuencia variable, como muestra la figura 2. El resorte está unido por un extremo al centro del parlante y el otro extremo está fijo. La tensión del resorte se ajusta variando su largo extendido. |
+ | : 4. Analice gráficamente la relación entre la tensión del resorte y la velocidad de propagación de las ondas. |
| − | : 2. Determine la constante elástica del resorte. |
||
| − | : 3. Conecte el amplificador de potencia y la interfaz ''PASCO'' del mismo modo que en el caso de las ondas transversales en la cuerda. <u>Mantenga el valor de voltaje en <math>5V</math></u> para la amplitud de oscilación. |
||
| − | : 4. Para distintos valores de la tensión del resorte, encuentre las frecuencias correspondientes a los modos normales de vibración, caracterizados por el número <math>n</math> correspondiente. |
||
| − | : 5. Usando gráficos de la forma <math>\omega</math> <math>versus</math> <math>n</math>, determine para las distintas tensiones la velocidad de propagación de ondas longitudinales en el resorte. |
+ | [[File:figura_3.png|center|thumb|500px|]] |
| − | : 6. Analice gráficamente la relación entre la tensión del resorte y la velocidad de propagación de las ondas. |
+ | == '''Adicionales''' == |
| + | Usando materiales asociados a los montajes previos, y algunos recursos extra disponibles en el laboratorio, usted podría estudiar: |
||
| + | : 1. Oscilaciones forzadas en un resorte o un péndulo |
||
| + | Utilizando el parlante como fuerza externa y un montaje apropiado, podría estudiar los cambios en la amplitud (A=A(<m>\omega</m>)), el angulo de fase (<m>\delta=\delta(\omega)</m>) y el efecto transiente de un resorte o un péndulo |
||
| + | : 2. Batido entre las ondas estacionarias y una luz estroboscópica |
||
| + | Utilizando una luz estroboscópica para iluminar la onda estacionaria y un cronómetro, podría medir las diferencias entre las frecuencias (<m>\Delta\omega</m>)de ambas fuentes (luz y generador de señales) |
||
| + | : 3. Propiedades de ondas estacionarias en cuerdas de densidad de masa variable |
||
| + | Utilizando distintas cuerdas unidas como medio de propagación (como hilos de pesca, disponibles en el lab), puede estudiar los cambios en la longitud de onda y (si es posible) los coeficientes de reflexión y transmisión de una onda |
||
| − | [[File:Ac3.png|center|thumb|500px|]] |
+ | En esta sección, usted debe elegir al menos uno de estos fenómenos para estudiar. Debe registrar en su Acta lo que está analizando, cómo lo hace, los inconvenientes y resultados obtenidos, análisis, etc. Si usted se le ocurre algo interesante de medir, dentro del contexto del curso, puede agregarlo a la lista de “Adicionales” |
Latest revision as of 14:39, 20 February 2018
Contents |
[edit] Ondas Estacionarias en 1-D
[edit] Objetivo
Estudiar ondas estacionarias en un medio 1-D
[edit] Introducción
El experimento consiste en el estudio de modos normales de vibración asociados a ondas estacionarias transversales y longitudinales en un medio 1-D.
Los modos normales de vibración asociados a ondas estacionarias en un medio 1-D de largo L, con ambos extremos fijos, tienen una elongación de la forma:
tanto para ondas transversales como para ondas longitudinales, cuyo número de onda viene dado por:
.
La frecuencia angular viene dada por:
Donde , y
es la velocidad de fase.
[edit] Procedimiento Experimental
Para ambos casos (ondas transversales y longitudinales) se usa el siguiente equipamiento:
- Generador de funciones.
- Parlante.
[edit] Determinación de las masas
- Mida la masa de la cuerda utilizando la balanza PL202-s
- Mida las masas utilizando la balanza PL3001-s
- Utilice los manuales de las balanzas para poder determinar errores sistematicos. En ellos podra encontrar información como se muestra a continuación:
Balanza: PL 3001-s
* Precisión minima: 0.1 gr * Repetición: 0.08 gr * linealidad: 0.2 gr
0.4 gr
[edit] Determinación de la constante elástica del resorte
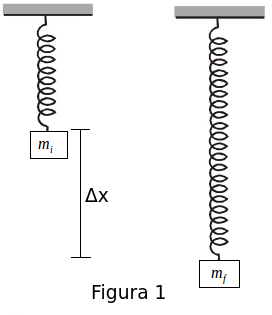
Para determinar la constante elástica coloque una masa en el resorte colgando de uno de sus extremos. Defina la posición de esta masa como origen de sistema de coordenadas o posición de referencia. Luego agregue otra masa al resorte (aumentando la masa) y mida el desplazamiento que se produce con respecto a la posición de referencia, como se muestra en la figura 1.
Utilizando la ecuación de equilibrio de fuerzas
Mediante métodos gráficos, considerando las barras de error apropiadas en cada caso, determine la constante del resorte.
[edit] Ondas Transversales
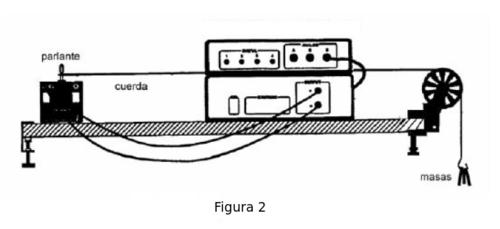
- 1. Las ondas son generadas en una cuerda excitada transversalmente por un parlante vibrando a frecuencia variable, como muestra la figura 2. La cuerda está unida por un extremo al centro del parlante, y en el otro extremo tiene un gancho para agregar masas, generando una tensión variable en el extremo libre.
- 2. La tensión de la cuerda se ajusta agregando golillas al gancho del extremo colgante. La tensión de la cuerda debe ser baja.
- 3. Mida la densidad lineal de masa de la cuerda.
- 4. Conecte el parlante al generador de funciones.
Warning: El o los botones atenuadores NO deben estar activos.
- 5. Para distintos valores de la tensión de la cuerda, encuentre las frecuencias correspondientes a los modos normales de vibración, caracterizados por el número
correspondiente.
- 6. Usando gráficos de la forma
, determine para las distintas tensiones la velocidad de propagación de ondas transversales en la cuerda.
- 7. Analice gráficamente la relación entre la tensión de la cuerda y la velocidad de propagación de las ondas.
[edit] Ondas Longitudinales
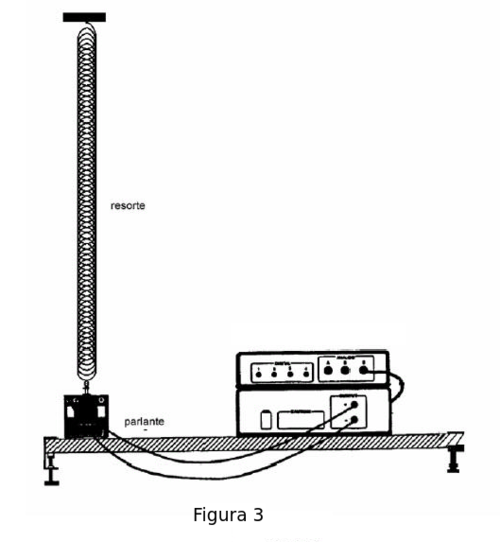
- 1. Las ondas son generadas en un resorte excitado longitudinalmente por un parlante vibrando a frecuencia variable, como muestra la figura 3. El resorte está unido por un extremo al centro del parlante y el otro extremo está fijo. La tensión del resorte se ajusta variando su largo extendido. Al igual que en el caso anterior la tensión del resorte debe ser baja.
- 2. Para distintos valores de la tensión del resorte, encuentre las frecuencias correspondientes a los modos normales de vibración, caracterizados por el número
correspondiente.
- 3. Usando gráficos de la forma
, determine para las distintas tensiones la velocidad de propagación de ondas longitudinales en el resorte.
- 4. Analice gráficamente la relación entre la tensión del resorte y la velocidad de propagación de las ondas.
[edit] Adicionales
Usando materiales asociados a los montajes previos, y algunos recursos extra disponibles en el laboratorio, usted podría estudiar:
- 1. Oscilaciones forzadas en un resorte o un péndulo
Utilizando el parlante como fuerza externa y un montaje apropiado, podría estudiar los cambios en la amplitud (A=A()), el angulo de fase (
) y el efecto transiente de un resorte o un péndulo
- 2. Batido entre las ondas estacionarias y una luz estroboscópica
Utilizando una luz estroboscópica para iluminar la onda estacionaria y un cronómetro, podría medir las diferencias entre las frecuencias ()de ambas fuentes (luz y generador de señales)
- 3. Propiedades de ondas estacionarias en cuerdas de densidad de masa variable
Utilizando distintas cuerdas unidas como medio de propagación (como hilos de pesca, disponibles en el lab), puede estudiar los cambios en la longitud de onda y (si es posible) los coeficientes de reflexión y transmisión de una onda
En esta sección, usted debe elegir al menos uno de estos fenómenos para estudiar. Debe registrar en su Acta lo que está analizando, cómo lo hace, los inconvenientes y resultados obtenidos, análisis, etc. Si usted se le ocurre algo interesante de medir, dentro del contexto del curso, puede agregarlo a la lista de “Adicionales”