File talk:Osciladores Acoplados (Fiz0312)
(→Introducción) |
m (Mfavre moved page Osciladores Acoplados (Fiz0312) to File talk:Osciladores Acoplados (Fiz0312)) |
||
| (5 intermediate revisions by 2 users not shown) | |||
| Line 3: | Line 3: | ||
===Objetivo=== |
===Objetivo=== |
||
| − | Estudiar la dinámica de osciladores acoplados, analizando cuantitativamente la existencia de modos normales de oscilacióm. |
+ | Estudiar la dinámica de osciladores acoplados, analizando cuantitativamente la existencia de modos normales de oscilación. |
| − | |||
===Introducción=== |
===Introducción=== |
||
| + | |||
| + | [[File:Ac1.png|right|thumb|400px| Figura 1]] |
||
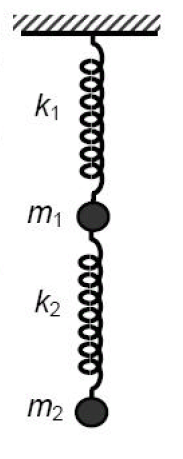
El experimento base consiste en el estudio de la dinámica de un sistema formado por dos masas acopladas mediante dos resortes, que oscilan a lo largo de la vertical. El montaje experimental se muestra esquemáticamente en la figura 1. |
El experimento base consiste en el estudio de la dinámica de un sistema formado por dos masas acopladas mediante dos resortes, que oscilan a lo largo de la vertical. El montaje experimental se muestra esquemáticamente en la figura 1. |
||
| Line 12: | Line 14: | ||
| − | :<center><math>m_1 \ddot{x}=-k_1x-k_2(x-y)</math></center> |
+ | :<center><m>m_1 \ddot{x}=-k_1x-k_2(x-y)</m></center> |
| − | :<center><math>m_2 \ddot{y}=k_2(x-y)</math></center> |
+ | :<center><m>m_2 \ddot{y}=k_2(x-y)</m></center> |
Suponiendo que ambas masas oscilan en un modo normal, buscamos condiciones para que las soluciones de las ecuaciones de movimiento tengan la forma: |
Suponiendo que ambas masas oscilan en un modo normal, buscamos condiciones para que las soluciones de las ecuaciones de movimiento tengan la forma: |
||
| − | :<center><math>x(t)=x_0 e^{i \omega t}</math></center> |
+ | :<center><m>x(t)=x_0 \cdot e^{i \omega t}</m></center> |
| − | :<center><math>y(t)=y_0 e^{i \omega t}</math></center> |
+ | :<center><m>y(t)=y_0 \cdot e^{i \omega t}</m></center> |
| Line 28: | Line 30: | ||
| − | : <math> |
+ | :<center><m> |
\begin{bmatrix} |
\begin{bmatrix} |
||
-m_1 \omega^2+k_1+k_2 & -k_2 \\ |
-m_1 \omega^2+k_1+k_2 & -k_2 \\ |
||
| Line 39: | Line 41: | ||
= |
= |
||
0 |
0 |
||
| − | </math> |
+ | </m></center> |
| + | |||
| + | |||
| + | De donde se obtiene que las frecuencias de los modos normales satisfacen la ecuación, |
||
| + | |||
| + | :<center><m>\omega^4-\frac{m_1 k_2+m_2(k_1+k_2)}{m_1 m_2}\omega^2+\frac{k_1 k_2}{m_1 m_2}=0</m> |
||
| + | |||
| + | === Procedimiento === |
||
| + | |||
| + | |||
| + | : 1. Mida los parámetros físicos del sistema: masas y constantes elásticas. |
||
| + | |||
| + | : 2. Construya un sistema de osciladores acoplados como muestra la figura 1. |
||
| + | |||
| + | : 3. A partir de los valores medidos, determine las frecuencias de ambos modos normales y la razón de amplitud de oscilación de ambas masas en cada uno de los modos normales. |
||
| + | |||
| + | : 4. Use el sistema ''Videocom'' para obtener mediciones de la oscilación de ambas masas para diferentes condiciones iniciales. |
||
| + | |||
| + | : 5. A partir de las mediciones anteriores, desacople los modos normales correspondientes. |
||
| + | |||
| + | : 6. Use las mediciones de oscilación para analizar la conservación de energía mecánica en el sistema. Note que para este análisis necesita mediciones de la velocidad de oscilación. |
||
| + | |||
| + | : 7. Si el tiempo y la motivación son suficientes, estudie otras configuraciones a osciladores acoplados verticales. Por ejemplo,tres masas con tres resortes. En este caso, debe resolver el problema de encontrar las frecuencias de modos normales y repetir, al menos en parte, el procedimiento anterior. |
||
Latest revision as of 15:00, 21 March 2019
Contents |
[edit] Osciladores Acoplados
[edit] Objetivo
Estudiar la dinámica de osciladores acoplados, analizando cuantitativamente la existencia de modos normales de oscilación.
[edit] Introducción
El experimento base consiste en el estudio de la dinámica de un sistema formado por dos masas acopladas mediante dos resortes, que oscilan a lo largo de la vertical. El montaje experimental se muestra esquemáticamente en la figura 1.
Considerando oscilaciones en torno a sus puntos de equilibrio, las ecuaciones de movimiento de las masas a lo largo de la vertical se escriben como:
Suponiendo que ambas masas oscilan en un modo normal, buscamos condiciones para que las soluciones de las ecuaciones de movimiento tengan la forma:
Reemplazando estas soluciones en las ecuaciones de movimiento, se obtiene que las amplitudes de oscilación en los modos normales satisfacen las ecuaciones
De donde se obtiene que las frecuencias de los modos normales satisfacen la ecuación,[edit] Procedimiento
- 1. Mida los parámetros físicos del sistema: masas y constantes elásticas.
- 2. Construya un sistema de osciladores acoplados como muestra la figura 1.
- 3. A partir de los valores medidos, determine las frecuencias de ambos modos normales y la razón de amplitud de oscilación de ambas masas en cada uno de los modos normales.
- 4. Use el sistema Videocom para obtener mediciones de la oscilación de ambas masas para diferentes condiciones iniciales.
- 5. A partir de las mediciones anteriores, desacople los modos normales correspondientes.
- 6. Use las mediciones de oscilación para analizar la conservación de energía mecánica en el sistema. Note que para este análisis necesita mediciones de la velocidad de oscilación.
- 7. Si el tiempo y la motivación son suficientes, estudie otras configuraciones a osciladores acoplados verticales. Por ejemplo,tres masas con tres resortes. En este caso, debe resolver el problema de encontrar las frecuencias de modos normales y repetir, al menos en parte, el procedimiento anterior.