Descarga de un Condensador (Fiz020)
(→Procedimiento) |
(→Procedimiento) |
||
| (5 intermediate revisions by 2 users not shown) | |||
| Line 20: | Line 20: | ||
Hasta aquí Ud. ha trabajado sólo con corrientes continuas que no varían en el tiempo. Las leyes obtenidas, en muchos casos, pueden aplicarse a corrientes variables, si la variación de la corriente no es demasiado rápida. |
Hasta aquí Ud. ha trabajado sólo con corrientes continuas que no varían en el tiempo. Las leyes obtenidas, en muchos casos, pueden aplicarse a corrientes variables, si la variación de la corriente no es demasiado rápida. |
||
| − | Efectivamente, supongamos que en un circuito con corriente continua la fuerza electromotriz (<math>\epsilon</math>) varía en una pequeña cantidad. La intensidad de la corriente en el circuito empieza a variar pero después de un cierto tiempo alcanza un nuevo valor constante. Variando <math>\epsilon</math> gradualmente creamos en el circuito una corriente que varía en forma análoga, a cuyos diversos valores son aplicables las leyes de al corriente continua. |
+ | Efectivamente, supongamos que en un circuito con corriente continua la fuerza electromotriz (<m>\epsilon</m>) varía en una pequeña cantidad. La intensidad de la corriente en el circuito empieza a variar pero después de un cierto tiempo alcanza un nuevo valor constante. Variando <m>\epsilon</m> gradualmente creamos en el circuito una corriente que varía en forma análoga, a cuyos diversos valores son aplicables las leyes de al corriente continua. |
| − | Supongamos ahora que incrementamos el número de los cambios graduales de <math>\epsilon</math> y reducimos, al mismo tiempo, su magnitud. Entonces, en el límite, obtenemos una fuerza electromotriz continuamente variable y análogamente para la corriente. |
+ | Supongamos ahora que incrementamos el número de los cambios graduales de <m>\epsilon</m> y reducimos, al mismo tiempo, su magnitud. Entonces, en el límite, obtenemos una fuerza electromotriz continuamente variable y análogamente para la corriente. |
Cuando un condensador cargado es conectado a una resistencia se produce una situación como la indicada anteriormente. Estudiaremos esta situación y obtendremos de ella un mejor conocimiento sobre el voltímetro que usamos. |
Cuando un condensador cargado es conectado a una resistencia se produce una situación como la indicada anteriormente. Estudiaremos esta situación y obtendremos de ella un mejor conocimiento sobre el voltímetro que usamos. |
||
| Line 29: | Line 29: | ||
=== Procedimiento === |
=== Procedimiento === |
||
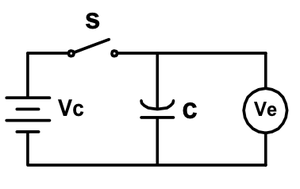
| − | En el circuito de la figura 1, <math>V_0</math> representa el voltaje de una fuente de C.C, C un condensador de capacidad conocida, S un interruptor normalmente desconectado y <math>V_e</math> un voltímetro de resistencia interna <math>R</math>. |
+ | En el circuito de la figura 1, <m>V_0</m> representa el voltaje de una fuente de C.C, C un condensador de capacidad conocida, S un interruptor normalmente desconectado y <m>V_e</m> un voltímetro de resistencia interna <m>R</m>. |
[[File:Cc3.png|center|thumb|300px| Figura 1: Montaje experimental.]] |
[[File:Cc3.png|center|thumb|300px| Figura 1: Montaje experimental.]] |
||
| − | Si se cierra el interruptor S de la fuente de C.C se carga el condensador <math>C</math> y el voltímetro indica, después de algunos instantes, el voltaje <math>V_0</math>. Si se abre el interruptor S el condensador <math>C</math> empieza a descargarse a través de la resistencia |
+ | Si se cierra el interruptor S de la fuente de C.C se carga el condensador <m>C</m> y el voltímetro indica, después de algunos instantes, el voltaje <m>V_0</m>. Si se abre el interruptor S el condensador <m>C</m> empieza a descargarse a través de la resistencia |
| − | interna del <math>V_e</math>. Consideremos la malla de la derecha. |
+ | interna del <m>V_e</m>. Consideremos la malla de la derecha. |
Sea, |
Sea, |
||
| − | :<math>I=−\frac{dq}{dt}</math> (1) |
+ | :<center><m>I=-\frac{dq}{dt} \qquad\qquad\qquad (1)</m></center> |
| Line 45: | Line 45: | ||
Sea, |
Sea, |
||
| − | :<math>V =qC</math> (2) |
+ | :<center><m>V =q \cdot C \qquad\qquad\qquad (2)</m></center> |
| − | el voltaje entre los bornes del condensador que tiene una carga <math>q</math> |
+ | el voltaje entre los bornes del condensador que tiene una carga <m>q</m> |
Sea, |
Sea, |
||
| − | :<math>V = R \cdot I</math> (3) |
+ | :<center><m>V = R \cdot I \qquad\qquad\qquad (3)</m> </center> |
el voltaje entre los bornes del voltímetro. A partir de las ecuaciones (1), (2) y (3) obtenga que |
el voltaje entre los bornes del voltímetro. A partir de las ecuaciones (1), (2) y (3) obtenga que |
||
| − | :<math>V = V_0 \cdot e^{−\frac{t}{RC}}</math> (4) |
+ | :<center><m>V = V_0 \cdot e^{-\frac{t}{RC}} \qquad\qquad\qquad (4)</m></center> |
| + | |||
| + | |||
: i) Arme el circuito indicado en al figura. Elija para el voltímetro una escala adecuada. |
: i) Arme el circuito indicado en al figura. Elija para el voltímetro una escala adecuada. |
||
| − | : ii) Conecte el interruptor S durante algunos segundos para cargar el condensador <math>C</math> sin abrir S lea <math>V_0</math> en el voltímetro. |
+ | : ii) Conecte el interruptor S durante algunos segundos para cargar el condensador <m>C</m> sin abrir S lea <m>V_0</m> en el voltímetro. |
: iii) Ponga en marcha su cronómetro justo en el instante en que Ud. abra elinterruptor S. |
: iii) Ponga en marcha su cronómetro justo en el instante en que Ud. abra elinterruptor S. |
||
| − | : iv) Confeccione una tabla de valores <math>V</math> versus t hasta que el condensador haya perdido un <math>90 \%</math> o un <math>95 \%</math> de su carga. |
+ | : iv) Confeccione una tabla de valores <m>V</m> versus t hasta que el condensador haya perdido un <m>90 \%</m> o un <m>95 \%</m> de su carga. |
=== Análisis y Preguntas === |
=== Análisis y Preguntas === |
||
| − | : 1) Gráfique V <math>versus</math> t en papel semilogaritmico. Explique como puede determinar la resistencia interna <math>R</math> a partir del gráfico. Calcúlela. |
+ | : 1) Gráfique V <m>versus</m> t en papel semilogaritmico. Explique como puede determinar la resistencia interna <m>R</m> a partir del gráfico. Calcúlela. |
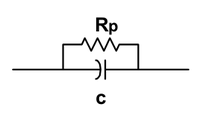
: 2) Un condensador real tiene “siempre” pérdidas y el símbolo adecuado para él es el siguiente: |
: 2) Un condensador real tiene “siempre” pérdidas y el símbolo adecuado para él es el siguiente: |
||
| Line 77: | Line 77: | ||
: donde Rp es la resistencia de pérdida. ¿De que manera afecta este hecho a su resultado?. |
: donde Rp es la resistencia de pérdida. ¿De que manera afecta este hecho a su resultado?. |
||
| − | : 3) ¿Cuál es la dimensión física del producto <math>RC</math>?, ¿Cuál es su significado físico? |
+ | : 3) ¿Cuál es la dimensión física del producto <m>RC</m>?, ¿Cuál es su significado físico? |
| − | : 4) Calcule el producto <math>RC</math> con sus datos. |
+ | : 4) Calcule el producto <m>RC</m> con sus datos. |
| − | : 5) Verifique lo calculado en su gráfico V <math>versus</math> t. |
+ | : 5) Verifique lo calculado en su gráfico V <m>versus</m> t. |
: 6) Resuma sus conclusiones. |
: 6) Resuma sus conclusiones. |
||
Latest revision as of 06:46, 28 October 2014
Contents |
[edit] Descarga de un Condensador
[edit] Objetivo
Estudiar empíricamente la existencia de constantes de tiempo características, asociadas a las capacidades en circuitos eléctricos.
[edit] Materiales
- - Condensador
- - Batería
- - Conectores
- - Multitester
[edit] Introducción
Hasta aquí Ud. ha trabajado sólo con corrientes continuas que no varían en el tiempo. Las leyes obtenidas, en muchos casos, pueden aplicarse a corrientes variables, si la variación de la corriente no es demasiado rápida.
Efectivamente, supongamos que en un circuito con corriente continua la fuerza electromotriz () varía en una pequeña cantidad. La intensidad de la corriente en el circuito empieza a variar pero después de un cierto tiempo alcanza un nuevo valor constante. Variando
gradualmente creamos en el circuito una corriente que varía en forma análoga, a cuyos diversos valores son aplicables las leyes de al corriente continua.
Supongamos ahora que incrementamos el número de los cambios graduales de y reducimos, al mismo tiempo, su magnitud. Entonces, en el límite, obtenemos una fuerza electromotriz continuamente variable y análogamente para la corriente.
Cuando un condensador cargado es conectado a una resistencia se produce una situación como la indicada anteriormente. Estudiaremos esta situación y obtendremos de ella un mejor conocimiento sobre el voltímetro que usamos.
[edit] Procedimiento
En el circuito de la figura 1, representa el voltaje de una fuente de C.C, C un condensador de capacidad conocida, S un interruptor normalmente desconectado y
un voltímetro de resistencia interna
.
Si se cierra el interruptor S de la fuente de C.C se carga el condensador y el voltímetro indica, después de algunos instantes, el voltaje
. Si se abre el interruptor S el condensador
empieza a descargarse a través de la resistencia
interna del
. Consideremos la malla de la derecha.
Sea,
la corriente que circula en el instante t
Sea,
el voltaje entre los bornes del condensador que tiene una carga
Sea,
el voltaje entre los bornes del voltímetro. A partir de las ecuaciones (1), (2) y (3) obtenga que
- i) Arme el circuito indicado en al figura. Elija para el voltímetro una escala adecuada.
- ii) Conecte el interruptor S durante algunos segundos para cargar el condensador
sin abrir S lea
en el voltímetro.
- iii) Ponga en marcha su cronómetro justo en el instante en que Ud. abra elinterruptor S.
- iv) Confeccione una tabla de valores
versus t hasta que el condensador haya perdido un
o un
de su carga.
[edit] Análisis y Preguntas
- 1) Gráfique V
t en papel semilogaritmico. Explique como puede determinar la resistencia interna
a partir del gráfico. Calcúlela.
- 2) Un condensador real tiene “siempre” pérdidas y el símbolo adecuado para él es el siguiente:
- donde Rp es la resistencia de pérdida. ¿De que manera afecta este hecho a su resultado?.
- 3) ¿Cuál es la dimensión física del producto
?, ¿Cuál es su significado físico?
- 4) Calcule el producto
con sus datos.
- 5) Verifique lo calculado en su gráfico V
t.
- 6) Resuma sus conclusiones.