Circuitos RC y LR (Fiz 153)
(→Preguntas) |
(→Preguntas) |
||
| (2 intermediate revisions by one user not shown) | |||
| Line 118: | Line 118: | ||
Al aplicar un voltaje continuo (DC) a un inductancia y una resistencia conectadas en serie, se establece una corriente estacionaria, dada por, |
Al aplicar un voltaje continuo (DC) a un inductancia y una resistencia conectadas en serie, se establece una corriente estacionaria, dada por, |
||
| − | :<center><math>I_{max}=\frac{V_0}{R} \qquad\qquad\qquad (3)</math> </center> |
+ | :<center><m>I_{max}=\frac{V_0}{R} \qquad\qquad\qquad (3)</m> </center> |
| − | donde <math>V_0</math> es el voltaje aplicado y <math>R</math> es la resistencia total del circuito. Para alcanzar esta condición estacionaria se requiere un cierto tiempo, dado que la inductancia produce una ''fem'' (fuerza electromotriz) en respuesta al incremento de corriente. La corriente del circuito aumenta exponencialmente, de acuerdo con la ecuación: |
+ | donde <m>V_0</m> es el voltaje aplicado y <m>R</m> es la resistencia total del circuito. Para alcanzar esta condición estacionaria se requiere un cierto tiempo, dado que la inductancia produce una ''fem'' (fuerza electromotriz) en respuesta al incremento de corriente. La corriente del circuito aumenta exponencialmente, de acuerdo con la ecuación: |
| − | :<center><math>I(t)=I_{max}(1-e^{-(R/L)t})=I_{max} \cdot (1-e^{-(t/\tau)}) \qquad\qquad\qquad (4)</math></center> |
+ | :<center><m>I(t)=I_{max}(1-e^{-(R/L)t})=I_{max} \cdot (1-e^{-(t/\tau)}) \qquad\qquad\qquad (4)</m></center> |
| − | donde <math>L</math> es la inductancia y <math>\tau = L/R</math> es la ''constante de tiempo inductiva''. Este valor |
+ | donde <m>L</m> es la inductancia y <m>\tau = L/R</m> es la ''constante de tiempo inductiva''. Este valor |
corresponde al tiempo que demora la corriente en aumentar a 63% de su valor máximo (o bajar a 37% de su máximo). El tiempo que demora la corriente en subir o bajar a la mitad de su máximo se relaciona con la constante de tiempo inductiva a través de: |
corresponde al tiempo que demora la corriente en aumentar a 63% de su valor máximo (o bajar a 37% de su máximo). El tiempo que demora la corriente en subir o bajar a la mitad de su máximo se relaciona con la constante de tiempo inductiva a través de: |
||
| − | :<center><math>t_{1/2}=\tau \cdot \ln{2} \qquad\qquad\qquad (5)</math></center> |
+ | :<center><m>t_{1/2}=\tau \cdot \ln{2} \qquad\qquad\qquad (5)</m></center> |
| − | Dado que el voltaje a través de la resistencia está dado por <math>V_R = I \cdot R</math>, el voltaje varía exponencialmente de acuerdo a la ecuación: |
+ | Dado que el voltaje a través de la resistencia está dado por <m>V_R = I \cdot R</m>, el voltaje varía exponencialmente de acuerdo a la ecuación: |
| − | :<center><math>V_R=V_0 \cdot (1-e^{-(t/\tau)}) \qquad\qquad\qquad (6)</math></center> |
+ | :<center><m>V_R=V_0 \cdot (1-e^{-(t/\tau)}) \qquad\qquad\qquad (6)</m></center> |
| − | Como el voltaje a través del la inductancia está dado por <math>V_L = L(dI/dt)</math>, este voltaje parte en <math>t = 0</math> en su valor máximo, y luego decrece exponencialmente: |
+ | Como el voltaje a través del la inductancia está dado por <m>V_L = L(dI/dt)</m>, este voltaje parte en <m>t = 0</m> en su valor máximo, y luego decrece exponencialmente: |
| − | :<center><math>V_L=V_0 \cdot e^{-(t/\tau)} \qquad\qquad\qquad (7)</math></center> |
+ | :<center><m>V_L=V_0 \cdot e^{-(t/\tau)} \qquad\qquad\qquad (7)</m></center> |
| − | Luego de un tiempo <math>t >> \tau</math>, se establece una corriente estacionaria <math>I_{max}</math> y el voltaje a través de la resistencia tiende al valor del voltaje aplicado <math>V_0</math>, es decir, el voltaje a través de la inductancia tiende a cero. En cualquier instante de tiempo se cumplen las Reglas de Kirchkoff. Es decir, la suma algebraica del voltaje en la resistencia más el voltaje en la inductancia debe ser cero. |
+ | Luego de un tiempo <m>t >> \tau</m>, se establece una corriente estacionaria <m>I_{max}</m> y el voltaje a través de la resistencia tiende al valor del voltaje aplicado <m>V_0</m>, es decir, el voltaje a través de la inductancia tiende a cero. En cualquier instante de tiempo se cumplen las Reglas de Kirchkoff. Es decir, la suma algebraica del voltaje en la resistencia más el voltaje en la inductancia debe ser cero. |
| − | |||
=== Montaje Experimental === |
=== Montaje Experimental === |
||
| Line 159: | Line 159: | ||
[[File:Rc4.png|right|thumb|300px|]] |
[[File:Rc4.png|right|thumb|300px|]] |
||
| − | : 1) Seleccione en los canales análogos A y B el '''Sensor de Voltaje'''. En el canal C seleccione '''Amplificador de Potencia'''. En la ventana del''' Generador de Señales''' fije la señal de onda cuadrada, de amplitud <math>3 V</math> y frecuencia <math>80 Hz</math>. Presione ''' Auto''' y cierre la ventana. |
+ | : 1) Seleccione en los canales análogos A y B el '''Sensor de Voltaje'''. En el canal C seleccione '''Amplificador de Potencia'''. En la ventana del''' Generador de Señales''' fije la señal de onda cuadrada, de amplitud <m>3 V</m> y frecuencia <m>80 Hz</m>. Presione ''' Auto''' y cierre la ventana. |
| − | : 2) Presione el botón '''Opciones''' y luego seleccione '''Detención Automática''', Tiempo, <math>0.02 seg</math>. Presione '''Aceptar'''. En el icono del sensor de voltaje seleccione la frecuencia de muestreo <math> 1000 Hz</math>, '''rápido'''. |
+ | : 2) Presione el botón '''Opciones''' y luego seleccione '''Detención Automática''', Tiempo, <m>0.02 seg</m>. Presione '''Aceptar'''. En el icono del sensor de voltaje seleccione la frecuencia de muestreo <m> 1000 Hz</m>, '''rápido'''. |
| − | : 3) En la opción '''Gráfico''', seleccione Canal A <math>versus</math> Tiempo y agregue los gráficos Canal B <math>versus</math> Tiempo, Voltaje de Salida <math>versus</math> Tiempo, y Canal C <math>versus</math> Tiempo. |
+ | : 3) En la opción '''Gráfico''', seleccione Canal A <m>versus</m> Tiempo y agregue los gráficos Canal B <m>versus</m> Tiempo, Voltaje de Salida <m>versus</m> Tiempo, y Canal C <m>versus</m> Tiempo. |
: 4) Encienda el amplificador de potencia y cierre el circuito.Presione '''INICIO''' para iniciar la recolección de datos. |
: 4) Encienda el amplificador de potencia y cierre el circuito.Presione '''INICIO''' para iniciar la recolección de datos. |
||
| Line 171: | Line 171: | ||
: 6) Encuentre la constante de tiempo inductiva usando los datos de corriente y tiempo. Encuentre el valor máximo de corriente y el tiempo en que el voltaje era cero. |
: 6) Encuentre la constante de tiempo inductiva usando los datos de corriente y tiempo. Encuentre el valor máximo de corriente y el tiempo en que el voltaje era cero. |
||
| − | <math>I_{max}</math> = _____________ <math>t_{V=0}</math> = _____________ |
+ | <m>I_{max}</m> = _____________ <m>t_{V=0}</m> = _____________ |
:: Encuentre el tiempo en que la corriente sube a la mitad del máximo. Anótelo, interpolando si ello resulta necesario. |
:: Encuentre el tiempo en que la corriente sube a la mitad del máximo. Anótelo, interpolando si ello resulta necesario. |
||
| − | ::: <math>t_{1/2}</math> = ______________ |
+ | ::: <m>t_{1/2}</m> = ______________ |
:: A partir de la diferencia entre ambos tiempos anteriores, encuentre el tiempo de vida media y, a partir de él, la constante de tiempo inductiva. |
:: A partir de la diferencia entre ambos tiempos anteriores, encuentre el tiempo de vida media y, a partir de él, la constante de tiempo inductiva. |
||
| − | <math>t_{1/2}</math> = _____________ <math>\tau</math> = _____________ |
+ | <m>t_{1/2}</m> = _____________ <m>\tau</m> = _____________ |
| − | |||
| − | : 7) Imprima los gráficos <math>V_L</math> (voltaje de la bobina) ''versus'' <math>tiempo</math>, <math>V_R</math> (voltaje de la resistencia) ''versus'' <math>tiempo</math> y <math>V_F</math> (voltaje de la fuente) ''versus'' <math>tiempo</math> |
||
| + | : 7) Imprima los gráficos <m>V_L</m> (voltaje de la bobina) ''versus'' <m>tiempo</m>, <m>V_R</m> (voltaje de la resistencia) ''versus'' <m>tiempo</m> y <m>V_F</m> (voltaje de la fuente) ''versus'' <m>tiempo</m> |
||
=== Preguntas === |
=== Preguntas === |
||
| − | * ¿Cómo se compara el valor medido de la constante de tiempo inductiva con el valor teórico dado por <math>\tau = L/R</math>? Recuerde que <math>R</math> representa la resistencia total del circuito. |
+ | * ¿Cómo se compara el valor medido de la constante de tiempo inductiva con el valor teórico dado por <m>\tau = L/R</m>? Recuerde que <m>R</m> representa la resistencia total del circuito. |
* ¿Se cumple la regla de Kirchoff? Compare al menos para tres tiempos distintos la suma algebraica del voltaje a través de la resistencia y la inductancia, con el voltaje de la fuente. Para esta comparación use los gráficos obtenidos anteriormente. |
* ¿Se cumple la regla de Kirchoff? Compare al menos para tres tiempos distintos la suma algebraica del voltaje a través de la resistencia y la inductancia, con el voltaje de la fuente. Para esta comparación use los gráficos obtenidos anteriormente. |
||
Latest revision as of 14:48, 23 October 2014
Contents |
[edit] Circuitos RC y LR
[edit] Objetivo
Estudiar empíricamente la existencia de constantes de tiempo características, asociadas a capacitancias e inductancias en circuitos eléctricos.
[edit] Equipamiento
- Computador PC con interfaz PASCO 6500
- Amplificador de Potencia, PASCO CI-6502
- Circuito RLC, PASCO CI-6512
- Conectores
- Interruptor
- Programa DATA STUDIO
[edit] Parte A: Circuito RC
[edit] Teoría
Al conectar un condensador descargado a una fuente de voltaje continuo, la razón a la cual se carga decrece con el tiempo. Al comienzo, el condensador se carga fácilmente, debido a que hay poca carga acumulada en sus placas, pero a medida que ésta se acumula, el voltaje debe realizar un mayor trabajo para mover cargas adicionales hacia las placas, para así vencer las fuerza repulsiva debida a acumulación de carga de igual signo. Como resultado de esto, la variación de carga en el condensador decae exponencialmente en el tiempo: rápidamente al principio, pero más lentamente a medida que transcurre el tiempo. La carga en las placas en un tiempo cualquiera, está dada por,
donde es la máxima carga en las placas y
es la constante de tiempo capacitiva (
, donde
es la resistencia y
la capacidad). Considerando límites extremos, note que cuando
,
, lo que significa que no hay carga inicial en las placas. Note también, que cuando
,
, lo que significa que toma tiempo infinito completar la carga del condensador.
El tiempo que toma la carga del condensador para alcanzar la mitad del máximo se llama tiempo de vida media, y se relaciona con la constante de tiempo a través de,
En este experimento la carga del condensador será medida de forma indirecta, midiendo el voltaje a través del condensador, dado que ambos son proporcionales:
[edit] Montaje Experimental
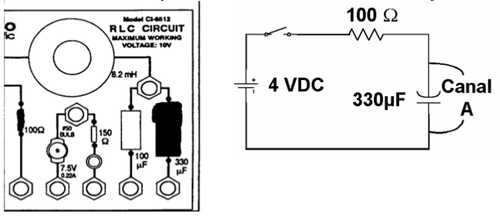
Usando la placa PASCO con componentes eléctricos, arme el circuito que muestra la figura 1, usando la salida del Amplificador de Potencia como fuente de voltaje.
| Precaución: Recuerde puentear la resistencia de con el condensador de omitir así, la participación de la inductancia. |
[edit] Procedimiento
- 1) Ponga en ejecución el programa Data Studio.
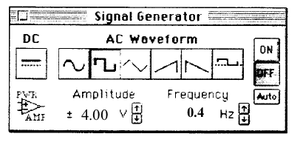
- 2) Para el canal A, seleccione del menú Sensor de Voltaje y para el canal C Amplificador de Potencia. En el icono del canal C aparecerá la ventana “Generador de Señales” .Seleccione la amplitud en
(voltaje del amplificador de potencia) la frecuencia de
y seleccione el botón de la señal AC de onda cuadrada. Cierre la ventana.
- 3) Presione el botón Options(Opciones) y luego seleccione Automatic Stop (Detención Automática), Tiempo, 2 seg, presione Aceptar. En el icono del sensor de voltaje seleccione la frecuencia de muestreo
, rápido
- 4) Active el osciloscopio y seleccione el canal A. Cambie la velocidad de barrido a
. Seleccione el icono A (Sensor de Voltaje).
- 5) Presione START (Inicio) y rápidamente cierre el circuito. Aparecerá en pantalla el voltaje a través del condensador. Este voltaje es proporcional a la carga del condensador, dado que
. Abra el circuito. Para obtener los datos, presione el icono Transfer (Transferir Datos.)

- 6) Para encontrar el tiempo de vida media, examine su tabla de datos. Para ello obtenga la Tabla de los datos obtenidos por el canal A.
- 7) Obtenga el Gráfico para ver la curva Voltaje vs Tiempo. Use las flechas de movimiento en la pantalla, para encontrar el punto en que el voltaje empieza a subir. Anote ese tiempo. Luego, muévase hasta el punto en que el voltaje alcanza la mitad del máximo (
). Anote este tiempo (interpole si es necesario).
= _____________
= _____________
- 8) Mida a continuación la resistencia con un ohmetro. Si dispone de un medidor de capacitancia, úselo para medir la capacitancia del condensador usado. En caso contrario, suponga que el valor correcto es
.
R = __________ C = __________
| Nota: El valor de la inductancia de la bobina con el núcleo es de |
[edit] Análisis de Datos
- a) Encuentre la diferencia entre ambos tiempos, para determinar el tiempo de vida media:
- b) Calcule el valor teórico, usando la Ecuación (2)
- c) Calcule la diferencia porcentual entre los valores teórico y experimental de
.
[edit] Preguntas
-
indica el tiempo que el condensador demora en cargarse a la mitad de la carga total. De acuerdo con esto, ¿Cuánto demora un condensador en alcanzar 75% de la carga total?
- Luego de cuatro vidas medias, ¿Qué porcentaje de la carga total ha alcanzado el condensador?
- ¿Cuál es la máxima carga, en términos de la carga total, que alcanza el condensador en este experimento?
[edit] Parte B: circuito LR
[edit] Teoría
Al aplicar un voltaje continuo (DC) a un inductancia y una resistencia conectadas en serie, se establece una corriente estacionaria, dada por,
donde es el voltaje aplicado y
es la resistencia total del circuito. Para alcanzar esta condición estacionaria se requiere un cierto tiempo, dado que la inductancia produce una fem (fuerza electromotriz) en respuesta al incremento de corriente. La corriente del circuito aumenta exponencialmente, de acuerdo con la ecuación:
donde es la inductancia y
es la constante de tiempo inductiva. Este valor
corresponde al tiempo que demora la corriente en aumentar a 63% de su valor máximo (o bajar a 37% de su máximo). El tiempo que demora la corriente en subir o bajar a la mitad de su máximo se relaciona con la constante de tiempo inductiva a través de:
Dado que el voltaje a través de la resistencia está dado por , el voltaje varía exponencialmente de acuerdo a la ecuación:
Como el voltaje a través del la inductancia está dado por , este voltaje parte en
en su valor máximo, y luego decrece exponencialmente:
Luego de un tiempo , se establece una corriente estacionaria
y el voltaje a través de la resistencia tiende al valor del voltaje aplicado
, es decir, el voltaje a través de la inductancia tiende a cero. En cualquier instante de tiempo se cumplen las Reglas de Kirchkoff. Es decir, la suma algebraica del voltaje en la resistencia más el voltaje en la inductancia debe ser cero.
[edit] Montaje Experimental
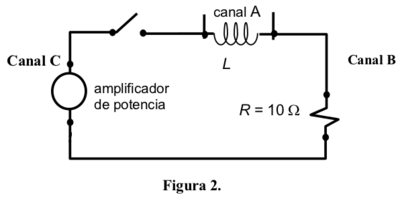
- i) Conecte el amplificador de potencia al canal C de la interfaz.
- ii) Conecte el circuito, como muestra la Figura 2, usando la señal de salida del amplificador de potencia como fuente DC.
- iii) Conecte el enchufe DIN al Canal A de la caja de interfaz. Conecte los enchufes banana a ambos extremos de la inductancia. Coloque el núcleo de hierro en el interior de la inductancia.
- iv) Ponga en ejecución el programa Data Studio.
[edit] Procedimiento
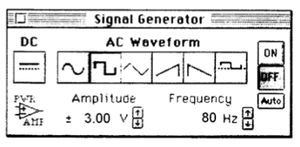
- 1) Seleccione en los canales análogos A y B el Sensor de Voltaje. En el canal C seleccione Amplificador de Potencia. En la ventana del Generador de Señales fije la señal de onda cuadrada, de amplitud
y frecuencia
. Presione Auto y cierre la ventana.
- 2) Presione el botón Opciones y luego seleccione Detención Automática, Tiempo,
. Presione Aceptar. En el icono del sensor de voltaje seleccione la frecuencia de muestreo
, rápido.
- 3) En la opción Gráfico, seleccione Canal A
Tiempo y agregue los gráficos Canal B
Tiempo, Voltaje de Salida
Tiempo, y Canal C
Tiempo.
- 4) Encienda el amplificador de potencia y cierre el circuito.Presione INICIO para iniciar la recolección de datos.
- 5) Examine el gráfico usando el cursor de movimiento en la pantalla
 , para obtener las coordenadas.
, para obtener las coordenadas.
- 6) Encuentre la constante de tiempo inductiva usando los datos de corriente y tiempo. Encuentre el valor máximo de corriente y el tiempo en que el voltaje era cero.
= _____________
= _____________
- Encuentre el tiempo en que la corriente sube a la mitad del máximo. Anótelo, interpolando si ello resulta necesario.
-
= ______________
-
- A partir de la diferencia entre ambos tiempos anteriores, encuentre el tiempo de vida media y, a partir de él, la constante de tiempo inductiva.
= _____________
= _____________
- 7) Imprima los gráficos
(voltaje de la bobina) versus
,
(voltaje de la resistencia) versus
y
(voltaje de la fuente) versus
[edit] Preguntas
- ¿Cómo se compara el valor medido de la constante de tiempo inductiva con el valor teórico dado por
? Recuerde que
representa la resistencia total del circuito.
- ¿Se cumple la regla de Kirchoff? Compare al menos para tres tiempos distintos la suma algebraica del voltaje a través de la resistencia y la inductancia, con el voltaje de la fuente. Para esta comparación use los gráficos obtenidos anteriormente.