Carga Específica del Electrón (Fiz0311)
(→Análisis) |
|||
| (4 intermediate revisions by 2 users not shown) | |||
| Line 27: | Line 27: | ||
| − | <center><math>B= \mu_0 (4/5)^{3/2} \cdot \frac{nI}{d/2} \qquad \qquad \qquad (1)</math></center> |
+ | <center><m>B= \mu_0 (4/5)^{3/2} \cdot \frac{nI}{d/2} \qquad \qquad \qquad (1)</m></center> |
donde : |
donde : |
||
| − | <math>B</math> : campo magnético |
+ | <m>B</m> : campo magnético |
| − | <math>\mu_0</math> : permeabilidad del vacío (<math>1.26 \cdot 10-6 \frac{Web}{A \cdot m }</math> |
+ | <m>\mu_0</m> : permeabilidad del vacío (<m>1.26 \times 10^{-6} \frac{Web}{A \cdot m })</m> |
| − | <math>n</math> : número de espiras de cada bobina |
+ | <m>n</m> : número de espiras de cada bobina |
| − | <math>I</math> : intensidad de la corriente |
+ | <m>I</m> : intensidad de la corriente |
| − | <math>d</math> : diámetro de las bobinas. |
+ | <m>d</m> : diámetro de las bobinas. |
Se puede obtener también el trabajo realizado al acelerar a un electrón desde el cátodo hasta el ánodo, lo que equivale a la energía cinética máxima del electrón : |
Se puede obtener también el trabajo realizado al acelerar a un electrón desde el cátodo hasta el ánodo, lo que equivale a la energía cinética máxima del electrón : |
||
| − | <center><math>e \cdot V = \frac{1}{2}m \cdot v^2 \qquad \qquad \qquad (2)</math></center> |
+ | <center><m>e \cdot V = \frac{1}{2}m \cdot v^2 \qquad \qquad \qquad (2)</m></center> |
| − | Si el electrón describe una trayectoria circular de radio “<math>r</math>”, estará sometido a una fuerza centrípeta <math>F_r</math> tal qué: |
+ | Si el electrón describe una trayectoria circular de radio “<m>r</m>”, estará sometido a una fuerza centrípeta <m>F_r</m> tal qué: |
| − | <center><math>F_r = \frac{m \cdot v^2}{r} \qquad \qquad \qquad (3)</math></center> |
+ | <center><m>F_r = \frac{m \cdot v^2}{r} \qquad \qquad \qquad (3)</m></center> |
| Line 57: | Line 57: | ||
| − | <center><math>F_r = B \cdot e \cdot v \qquad \qquad \qquad (4)</math></center> |
+ | <center><m>F_r = B \cdot e \cdot v \qquad \qquad \qquad (4)</m></center> |
de (3) y (4) tenemos : |
de (3) y (4) tenemos : |
||
| − | <center><math>\frac{m \cdot v^2}{r} = B \cdot e \cdot v </math></center> |
+ | <center><m>\frac{m \cdot v^2}{r} = B \cdot e \cdot v </m></center> |
luego, |
luego, |
||
| − | <center><math>v= \frac{e}{m}B \cdot r </math></center> |
+ | <center><m>v= \frac{e}{m}B \cdot r </m></center> |
| − | despejando <math>v</math> de la ec. (2) : |
+ | despejando <m>v</m> de la ec. (2) : |
| − | <center><math>v= \sqrt{\frac{2e \cdot V}{m}} </math></center> |
+ | <center><m>v= \sqrt{\frac{2e \cdot V}{m}} </m></center> |
entonces : |
entonces : |
||
| − | <center><math> \frac{e}{m}B \cdot r = \sqrt{\frac{2e \cdot V}{m}} </math></center> |
+ | <center><m> \frac{e}{m}B \cdot r = \sqrt{\frac{2e \cdot V}{m}} </m></center> |
| Line 83: | Line 83: | ||
| − | <center><math> \frac{e}{m} = \frac{2V}{B^2 \cdot r^2} </math></center> |
+ | <center><m> \frac{e}{m} = \frac{2V}{B^2 \cdot r^2} </m></center> |
| Line 91: | Line 91: | ||
Este aparato es un tubo de rayos catódicos especialmente adaptado para obtener un haz de electrones concentrado. Así es posible observar claramente los efectos que ejercen los campos eléctricos y magnéticos sobre el haz de electrones. |
Este aparato es un tubo de rayos catódicos especialmente adaptado para obtener un haz de electrones concentrado. Así es posible observar claramente los efectos que ejercen los campos eléctricos y magnéticos sobre el haz de electrones. |
||
| − | El T.R.E.F. contiene hidrógeno a una presión de <math>10^{-2}</math> mm de Hg, de ésta forma la carga espacial producida por el haz catódico en el volumen gaseoso concentra el haz.(fig.1) |
+ | El T.R.E.F. contiene hidrógeno a una presión de <m>10^{-2}</m> mm de Hg, de ésta forma la carga espacial producida por el haz catódico en el volumen gaseoso concentra el haz.(fig.1) |
| Line 101: | Line 101: | ||
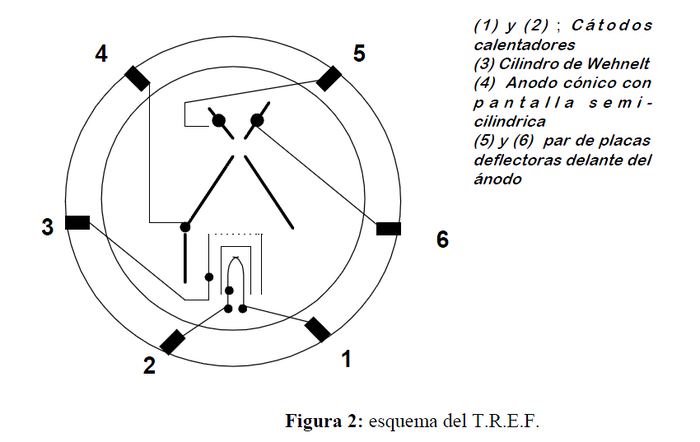
El tubo de rayos catódicos tiene un sistema de rayos electrónicos consistente en un cátodo de óxido indirectamente calentado, un cilindro de Wehnelt y un ánodo; tiene montado un par de placas para la desviación electrostática de los rayos. Las conexiones de los electrodos y de las placas de desviación se hacen por medio de una zócalo de seis polos. La presión existente en el tubo se ha regulado de tal modo que el rayo de |
El tubo de rayos catódicos tiene un sistema de rayos electrónicos consistente en un cátodo de óxido indirectamente calentado, un cilindro de Wehnelt y un ánodo; tiene montado un par de placas para la desviación electrostática de los rayos. Las conexiones de los electrodos y de las placas de desviación se hacen por medio de una zócalo de seis polos. La presión existente en el tubo se ha regulado de tal modo que el rayo de |
||
| − | electrones generado por éste sistema sea intensamente concentrado y definido en toda su longitud a una tensión anódica de <math>200 V-300 V</math>. |
+ | electrones generado por éste sistema sea intensamente concentrado y definido en toda su longitud a una tensión anódica de <m>200 V-300 V</m>. |
| − | La bobina de Helmholtz se compone de 2 bobinas sencillas, cada una de <math>130</math> espiras y <math>150 mm</math> de radio, a una distancia, una de otra de <math>150 mm</math>. Puede soportar hasta <math>5A</math> de corriente. |
+ | La bobina de Helmholtz se compone de 2 bobinas sencillas, cada una de <m>130</m> espiras y <m>150 mm</m> de radio, a una distancia, una de otra de <m>150 mm</m>. Puede soportar hasta <m>5A</m> de corriente. |
| Line 109: | Line 109: | ||
'''Características de trabajo:''' |
'''Características de trabajo:''' |
||
| − | * Tensión del filamento : <math>6.3 V</math> AC. (corriente alterna) o DC. (corriente directa) |
+ | * Tensión del filamento : <m>6.3 V</m> AC. (corriente alterna) o DC. (corriente directa) |
| − | * Tensión de Wehnelt : <math>0V</math> a <math>6 V</math> DC.positiva con respecto al cátodo. |
+ | * Tensión de Wehnelt : <m>0V</m> a <m>6 V</m> DC.positiva con respecto al cátodo. |
| − | * Tensión del ánodo : <math>150V</math> a <math>200V</math> CC. variable. |
+ | * Tensión del ánodo : <m>150V</m> a <m>200V</m> CC. variable. |
| − | * Fuente de poder requerida para producir el campo magnético en las bobinas de Helmholtz : <math>6V</math>; <math>0A-2A</math> |
+ | * Fuente de poder requerida para producir el campo magnético en las bobinas de Helmholtz : <m>6V</m>; <m>0A-2A</m> |
[[File:Tub2.png|center|thumb|700px| ]] |
[[File:Tub2.png|center|thumb|700px| ]] |
||
| − | |||
| − | |||
===Procedimiento=== |
===Procedimiento=== |
||
| Line 130: | Line 128: | ||
| − | : 2. Asegúrese de que el filamento del cátodo caliente esté alimentado con <math>6.3 V</math>. |
+ | : 2. Asegúrese de que el filamento del cátodo caliente esté alimentado con <m>6.3 V</m>. |
| − | : 3. El ánodo debe alimentarse con <math>150 V</math> DC aprox. Cuando el cátodo comience a brillar aumente el voltaje del ánodo, hasta que el haz de electrones se vea lo más nítido posible. |
+ | : 3. El ánodo debe alimentarse con <m>150 V</m> DC aprox. Cuando el cátodo comience a brillar aumente el voltaje del ánodo, hasta que el haz de electrones se vea lo más nítido posible. |
| − | : 4. Aplique corriente a las bobinas ( hasta <math>2 A</math>) |
+ | : 4. Aplique corriente a las bobinas ( hasta <m>2 A</m>) |
: 5. Mida el diámetro de la trayectoria circular del rayo electrónico dentro del campo. |
: 5. Mida el diámetro de la trayectoria circular del rayo electrónico dentro del campo. |
||
| Line 155: | Line 153: | ||
* Calcule la velocidad de los electrones para los voltajes del ánodo usado. |
* Calcule la velocidad de los electrones para los voltajes del ánodo usado. |
||
| − | * Obtenga el valor promedio para la razón <math>e/m</math> según los datos obtenidos durante la experiencia. Discuta el resultado |
+ | * Obtenga el valor promedio para la razón <m>e/m</m> según los datos obtenidos durante la experiencia. Discuta el resultado |
| − | * Confeccione un gráfico Potencial de aceleración (<math>V</math>) v/s el cuadrado del radio de la trayectoria (<math>r^2</math> ). Interprete. |
+ | * Confeccione un gráfico Potencial de aceleración (<m>V</m>) v/s el cuadrado del radio de la trayectoria (<m>r^2</m> ). Interprete. |
| − | * razón <math>e/m</math>, Ud. podría encontrar la masa de un electrón, si se conociera la carga. ¿Cómo podría la carga de un electrón ser medida? Discuta los efectos del campo magnético terrestre en los resultados del experimento. |
+ | * razón <m>e/m</m>, Ud. podría encontrar la masa de un electrón, si se conociera la carga. ¿Cómo podría la carga de un electrón ser medida? Discuta los efectos del campo magnético terrestre en los resultados del experimento. |
* ¿Cómo varía el diámetro del haz de electrones con el campo magnético presente, para un potencial constante del ánodo?. |
* ¿Cómo varía el diámetro del haz de electrones con el campo magnético presente, para un potencial constante del ánodo?. |
||
| − | * Discuta otro método para determinar la razón <math>e/m</math>. |
+ | * Discuta otro método para determinar la razón <m>e/m</m>. |
Latest revision as of 07:08, 23 October 2014
Contents |
[edit] Determinación del cuociente e/m ( carga eléctrica y masa del electrón)
[edit] Objetivo
Obtener un valor aproximado para el cuociente e/m (carga eléctrica/masa del electrón).
[edit] Materiales
- Tubo de rayo electrónico filiforme (T.R.E.F.)
- Fuente de alimentación del tubo
- Fuente variable de corriente continua (alimentación bobinas)
- 2 multitester
[edit] Teoría
Un haz de electrones se desvía siguiendo una trayectoria circular cuando se desplaza en un campo magnético perpendicular a la dirección del movimiento inicial.
Para el caso de dos bobinas paralelas (Bobinas de Helmholtz), separadas por una distancia igual a su radio y alimentadas por la misma corriente (girando en el mismo sentido), podemos determinar el campo magnético entre ambas.
Usando la Ley de Biot-Savart :
donde :
: campo magnético
: permeabilidad del vacío (
: número de espiras de cada bobina
: intensidad de la corriente
: diámetro de las bobinas.
Se puede obtener también el trabajo realizado al acelerar a un electrón desde el cátodo hasta el ánodo, lo que equivale a la energía cinética máxima del electrón :
Si el electrón describe una trayectoria circular de radio “”, estará sometido a una fuerza centrípeta
tal qué:
determinada por la influencia. Esta fuerza puede ser calculada en este caso (campo perpendicular al desplazamiento de los electrones) por la relación :
de (3) y (4) tenemos :
luego,
despejando de la ec. (2) :
entonces :
finalmente se obtiene:
Descripción del Aparato : Tubo de rayo electrónico filiforme (T.R.E.F.).
Este aparato es un tubo de rayos catódicos especialmente adaptado para obtener un haz de electrones concentrado. Así es posible observar claramente los efectos que ejercen los campos eléctricos y magnéticos sobre el haz de electrones.
El T.R.E.F. contiene hidrógeno a una presión de mm de Hg, de ésta forma la carga espacial producida por el haz catódico en el volumen gaseoso concentra el haz.(fig.1)
Tal concentración depende también de la velocidad de los electrones y de la densidad del flujo de éstos. La presencia del hidrógeno hace visible la trayectoria del haz.
El tubo de rayos catódicos tiene un sistema de rayos electrónicos consistente en un cátodo de óxido indirectamente calentado, un cilindro de Wehnelt y un ánodo; tiene montado un par de placas para la desviación electrostática de los rayos. Las conexiones de los electrodos y de las placas de desviación se hacen por medio de una zócalo de seis polos. La presión existente en el tubo se ha regulado de tal modo que el rayo de
electrones generado por éste sistema sea intensamente concentrado y definido en toda su longitud a una tensión anódica de .
La bobina de Helmholtz se compone de 2 bobinas sencillas, cada una de espiras y
de radio, a una distancia, una de otra de
. Puede soportar hasta
de corriente.
Características de trabajo:
- Tensión del filamento :
AC. (corriente alterna) o DC. (corriente directa)
- Tensión de Wehnelt :
a
DC.positiva con respecto al cátodo.
- Tensión del ánodo :
a
CC. variable.
- Fuente de poder requerida para producir el campo magnético en las bobinas de Helmholtz :
;
[edit] Procedimiento
- 1. Arme el montaje de la figura 3.
- 2. Asegúrese de que el filamento del cátodo caliente esté alimentado con
.
- 3. El ánodo debe alimentarse con
DC aprox. Cuando el cátodo comience a brillar aumente el voltaje del ánodo, hasta que el haz de electrones se vea lo más nítido posible.
- 4. Aplique corriente a las bobinas ( hasta
)
- 5. Mida el diámetro de la trayectoria circular del rayo electrónico dentro del campo.
- NOTA: utilice una regla para medir el diámetro de la trayectoria. Para ello debe medir dos posiciones opuestas de la trayectoria. Puede tomar una foto con una cámara fotográfica digital
- 6. Varíe la tensión de aceleración V y confeccione una tabla de valores como la siguiente.
- 7. Suavemente gire el tubo y observe el haz de electrones cuando la velocidad de los electrones no sea perpendicular al campo magnético.
[edit] Análisis
- Calcule la velocidad de los electrones para los voltajes del ánodo usado.
- Obtenga el valor promedio para la razón
según los datos obtenidos durante la experiencia. Discuta el resultado
- Confeccione un gráfico Potencial de aceleración (
) v/s el cuadrado del radio de la trayectoria (
). Interprete.
- razón
, Ud. podría encontrar la masa de un electrón, si se conociera la carga. ¿Cómo podría la carga de un electrón ser medida? Discuta los efectos del campo magnético terrestre en los resultados del experimento.
- ¿Cómo varía el diámetro del haz de electrones con el campo magnético presente, para un potencial constante del ánodo?.
- Discuta otro método para determinar la razón
.