Sistemas de Poleas (Fis 151/Fis 1513)
(Created page with "==Sistemas de Poleas== ===Objetivo=== Estudiar y aplicar el funcionamiento de un sistema de poleas. ===Introducción=== La variedad de aplicaciones que presenta el funciona…") |
(→Análisis) |
||
| (4 intermediate revisions by 2 users not shown) | |||
| Line 53: | Line 53: | ||
| − | 4.-Desplace un colgante una cierta distancia, mídala (<math>h_1</math>). Mida el desplazamiento del otro colgante (<math>h_2</math>) con respecto al punto inicial. |
+ | 4.-Desplace un colgante una cierta distancia, mídala (<m>h_1</m>). Mida el desplazamiento del otro colgante (<m>h_2</m>) con respecto al punto inicial. |
5.- Cuelgue masas en ambos colgantes hasta dejar el sistema en equilibrio. Anote el valor de estas masas (Figura 2) para 2 configuraciones distintas. |
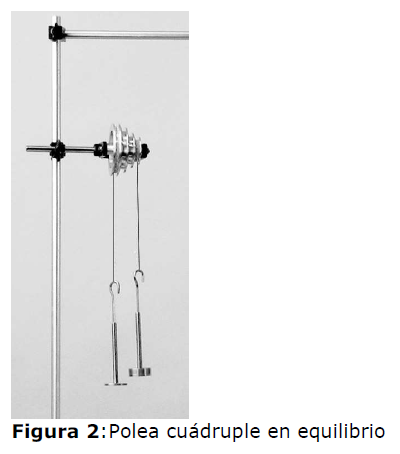
5.- Cuelgue masas en ambos colgantes hasta dejar el sistema en equilibrio. Anote el valor de estas masas (Figura 2) para 2 configuraciones distintas. |
||
| Line 66: | Line 66: | ||
: 1.- A partir de la experiencia realizada con la polea 4 pasos y con los datos obtenidos, encuentre la razón entre los radios de las poleas utilizadas. |
: 1.- A partir de la experiencia realizada con la polea 4 pasos y con los datos obtenidos, encuentre la razón entre los radios de las poleas utilizadas. |
||
| − | 2.- Encuentre la razón entre los desplazamientos. |
+ | : 2.- Encuentre la razón entre los desplazamientos. |
| − | 3.- Cuando el sistema se encuentra en equilibrio, encuentre la relación entre las masas colgantes. Compare esta relación con la de los radios y la de los desplazamientos. |
+ | : 3.- Cuando el sistema se encuentra en equilibrio, encuentre la relación entre las masas colgantes. Compare esta relación con la de los radios y la de los desplazamientos. |
: 4.- A partir de los estudios realizados en los puntos anteriores del análisis. ¿Cuál es la interpretación física que Ud. le daría a las relaciones obtenidas de este sistema de poleas?. Fundamente. |
: 4.- A partir de los estudios realizados en los puntos anteriores del análisis. ¿Cuál es la interpretación física que Ud. le daría a las relaciones obtenidas de este sistema de poleas?. Fundamente. |
||
| − | |||
| − | |||
| − | |||
==Experimento II: “El Polipasto”== |
==Experimento II: “El Polipasto”== |
||
| Line 100: | Line 97: | ||
- cuerda |
- cuerda |
||
| − | - Sensor de Fuerza, <math>50 N</math> (''Pasco'') |
+ | - Sensor de Fuerza, <m>50 N</m> (''Pasco'') |
| − | - 1 Dinamómetro de 10 N<math>Escribir la fórmula aquí</math> |
+ | - 1 Dinamómetro de 10 N <m>Escribir la formula aqui</m> |
| − | - Masa de <math>500 gr</math>. |
+ | - Masa de <m>500 gr</m>. |
- Balanza digital |
- Balanza digital |
||
| Line 111: | Line 108: | ||
- Computador con programa ''Data Studio''. |
- Computador con programa ''Data Studio''. |
||
| − | |||
===Procedimiento=== |
===Procedimiento=== |
||
| Line 125: | Line 121: | ||
| − | 3.- En el otro extremo de la cuerda ate un dinamómetro de <math>10 N</math>, el cual medirá la fuerza externa aplicada al sistema. (ver figura 6) |
+ | 3.- En el otro extremo de la cuerda ate un dinamómetro de <m>10 N</m>, el cual medirá la fuerza externa aplicada al sistema. (ver figura 6) |
[[File:Pol6.png|center|thumb|500px| ]] |
[[File:Pol6.png|center|thumb|500px| ]] |
||
| Line 143: | Line 139: | ||
: 1.- En el mismo programa, obtenga el gráfico Fuerza sensor vs fuerza dinamómetro. Interprete físicamente el valor de la pendiente. |
: 1.- En el mismo programa, obtenga el gráfico Fuerza sensor vs fuerza dinamómetro. Interprete físicamente el valor de la pendiente. |
||
| − | : 2.- Reemplace el sensor de Fuerza por una masa de <math>500 gr</math>. En base al punto anterior calcule la masa que se necesita para levantar los 500 gr. |
+ | : 2.- Reemplace el sensor de Fuerza por una masa de <m>500 gr</m>. En base al punto anterior calcule la masa que se necesita para levantar los 500 gr. |
: 3.-¿Puede encontrar alguna relación entre la fuerza aplicada y el numero de poleas que conforman el polipasto para levantar una cierta masa? |
: 3.-¿Puede encontrar alguna relación entre la fuerza aplicada y el numero de poleas que conforman el polipasto para levantar una cierta masa? |
||
| Line 152: | Line 148: | ||
| − | ==Experimento III: “ Cálculo de <math>g</math>”== |
+ | ==Experimento III: “ Cálculo de <m>g</m>”== |
| Line 162: | Line 158: | ||
===Introducción=== |
===Introducción=== |
||
| − | En esta experiencia se utilizará una polea de dos pasos, la cual conforma el Sensor de movimiento Rotacional, con el cual se procederá a variar la masa del sistema y medir las variables del movimiento rotacional que permitirá comprobar el valor de <math>g</math>. |
+ | En esta experiencia se utilizará una polea de dos pasos, la cual conforma el Sensor de movimiento Rotacional, con el cual se procederá a variar la masa del sistema y medir las variables del movimiento rotacional que permitirá comprobar el valor de <m>g</m>. |
| Line 171: | Line 167: | ||
| − | <center><math>R_1 \cdot T_1 - R_2 \cdot T_2 = I \cdot \alpha</math></center> |
+ | <center><m>R_1 \cdot T_1 - R_2 \cdot T_2 = I \cdot \alpha</m></center> |
| Line 177: | Line 173: | ||
| − | <center><math>I = M \cdot R_1^2 + M \cdot R_2 ^2</math></center> |
+ | <center><m>I = M \cdot R_1^2 + M \cdot R_2 ^2</m></center> |
| − | siendo <math>M</math> la masa de las poleas, y considerándola despreciable (<math>M \approx 0</math>) |
+ | siendo <m>M</m> la masa de las poleas, y considerándola despreciable (<m>M \approx 0</m>) |
Luego |
Luego |
||
| − | <center><math>R_1 \cdot T_1 = R_2 \cdot T_2</math></center> |
+ | <center><m>R_1 \cdot T_1 = R_2 \cdot T_2</m></center> |
| − | <center><math>\Rightarrow \frac{R_1}{R_2} = \frac{T_2}{T_1} \qquad \qquad \qquad (1)</math></center> |
+ | <center><m>\Rightarrow \frac{R_1}{R_2} = \frac{T_2}{T_1} \qquad \qquad \qquad (1)</m></center> |
| Line 193: | Line 189: | ||
| − | <center><math>m_1 \cdot g - T_1 = m_1 \cdot a_1 \qquad \qquad \qquad (2)</math></center> |
+ | <center><m>m_1 \cdot g - T_1 = m_1 \cdot a_1 \qquad \qquad \qquad (2)</m></center> |
| − | <center><math>m_2 \cdot g - T_2 = m_2 \cdot a_2 \qquad \qquad \qquad (3)</math></center> |
+ | <center><m>m_2 \cdot g - T_2 = m_2 \cdot a_2 \qquad \qquad \qquad (3)</m></center> |
| Line 202: | Line 198: | ||
| − | <center><math>a_2 = - a_1 \frac{R_2}{R_1} </math></center> |
+ | <center><m>a_2 = - a_1 \frac{R_2}{R_1} </m></center> |
| − | <center><math>m_2 \cdot g - \frac{R_1}{R_2} \cdot T__1 = m_2 \cdot \left(- a_1 \cdot \frac{R_2}{R_1} \right) \qquad \qquad \qquad (4)</math></center> |
+ | <center><m>m_2 \cdot g - \frac{R_1}{R_2} \cdot T_1 = m_2 \cdot \left( - a_1 \cdot \frac{R_2}{R_1} \right) \qquad \qquad \qquad (4)</m></center> |
| − | donde <math>a_1=R_1 \alpha</math>. Despejando <math>\alpha</math>, se obtiene |
+ | donde <m>a_1=R_1 \alpha</m>. Despejando <m>\alpha</m>, se obtiene |
| − | <center><math>\alpha = \frac{g \cdot (m_1 \cdot R_1 - m_2 \cdot R_2)}{m_1 \cdot R_1^2 + m_2 \cdot R_2^2} </math></center> |
+ | <center><m>\alpha = \frac{g \cdot (m_1 \cdot R_1 - m_2 \cdot R_2)}{m_1 \cdot R_1^2 + m_2 \cdot R_2^2} </m></center> |
| Line 238: | Line 234: | ||
: 3.- Cuando amarre los hilos en las poleas, asegúrese que los nudos queden por detrás de ésta, para no trancar el movimiento. |
: 3.- Cuando amarre los hilos en las poleas, asegúrese que los nudos queden por detrás de ésta, para no trancar el movimiento. |
||
| − | : 4.- En el programa ''Data Studio'' seleccione el sensor rotacional. En el mismo icono de este sensor seleccione la medición que realizará el sensor, rapidez angular y la frecuencia de muestreo, <math>10 Hz</math>. |
+ | : 4.- En el programa ''Data Studio'' seleccione el sensor rotacional. En el mismo icono de este sensor seleccione la medición que realizará el sensor, rapidez angular y la frecuencia de muestreo, <m>10 Hz</m>. |
| Line 249: | Line 245: | ||
: 7.- Realice la experiencia nuevamente para 5 pares diferentes de masas colgantes. Repita el punto 6 para cada experiencia. Realice una tabla como la siguiente: |
: 7.- Realice la experiencia nuevamente para 5 pares diferentes de masas colgantes. Repita el punto 6 para cada experiencia. Realice una tabla como la siguiente: |
||
| + | |||
| + | |||
| + | [[File:Pol9.png|center|thumb|700px| ]] |
||
| + | |||
| + | |||
| + | 8.- Usando Excel, realice una gráfica de las aceleraciones angulares obtenidas en el punto <m>7</m> ''versus'' <m>\frac{m_1 R_1 - m_2 R_2}{m_1 R_1^2 + m_2 R_2^2}</m> . Interprete físicamente el valor de la pendiente obtenida. |
||
Latest revision as of 06:31, 29 October 2014
Contents |
[edit] Sistemas de Poleas
[edit] Objetivo
Estudiar y aplicar el funcionamiento de un sistema de poleas.
[edit] Introducción
La variedad de aplicaciones que presenta el funcionamiento de los sistemas de maquinas simples y compuestas conduce a lo importante que es descubrir y conocer sus principios de funcionamiento y de este modo ampliar el rol que cumple la física en este y otros campos de la ciencia y la tecnología.
En estas experiencias se utilizarán diversos tipos de poleas. Estas se utilizan normalmente para cambiar la dirección de las fuerzas, siendo más fácil levantar la carga.
[edit] Experimento I: “Estudio de Reducción en un sistema de Poleas”
[edit] Objetivo:
Analizar y comprender intuitivamente la relación existenteentre las diversas variables físico-matemáticas presentes en un sistema de poleas.
[edit] Materiales
- Polea 4 pasos
- 2 trozos de cuerdas
- 2 ganchos con pesas
- Balanza digital
- Sistema base para colgar poleas
[edit] Procedimiento
- 1.- Arme el sistema que indica la figura 0, utilizando una polea 4 pasos. Pegar una huincha en la varilla izquierda del sistema.
2.- Arme 2 colgantes con pesas, y luego máselos en una balanza digital.
3.- Escoja dos poleas a utilizar. Con un pie de metro mida sus diámetros. Enrolle las cuerdas, en sentido contrario una con respecto a la otra, en cada una de ellas (figura 1).
4.-Desplace un colgante una cierta distancia, mídala (). Mida el desplazamiento del otro colgante (
) con respecto al punto inicial.
5.- Cuelgue masas en ambos colgantes hasta dejar el sistema en equilibrio. Anote el valor de estas masas (Figura 2) para 2 configuraciones distintas.
[edit] Análisis
- 1.- A partir de la experiencia realizada con la polea 4 pasos y con los datos obtenidos, encuentre la razón entre los radios de las poleas utilizadas.
- 2.- Encuentre la razón entre los desplazamientos.
- 3.- Cuando el sistema se encuentra en equilibrio, encuentre la relación entre las masas colgantes. Compare esta relación con la de los radios y la de los desplazamientos.
- 4.- A partir de los estudios realizados en los puntos anteriores del análisis. ¿Cuál es la interpretación física que Ud. le daría a las relaciones obtenidas de este sistema de poleas?. Fundamente.
[edit] Experimento II: “El Polipasto”
[edit] Objetivo:
Analizar y comprender intuitivamente la relación existente entre las diversas variables físico-matemáticas presentes en un sistema de poleas.
[edit] Introducción
En esta experiencia se utilizará un polipasto, que es un sistema formado por poleas fijas y poleas móviles, las cuales están distribuidas y sujetas a través de cuerdas, el cual se usa para levantar una masa determinada, pero realizando un esfuerzo menor. El polipasto es una combinación de poleas fijas y móviles recorridas por una sola cuerda que tiene uno de sus extremos anclado a un punto fijo.
- Los elementos de este sistema son los siguientes:
La polea fija tiene la función de modificar la dirección de la fuerza externa a ejercer sobre la cuerda. La polea móvil tiene la función de proporcionar ganancia mecánica al sistema. La cuerda transmite las fuerzas entre los diferentes elementos. Su resistencia a la tracción ha de estar en función del valor de la resistencia y de la ganancia mecánica del sistema, que a su vez depende del número de poleas móviles y de su combinación con las fijas.
[edit] Materiales
- Polipasto de 6 poleas
- cuerda
- Sensor de Fuerza, (Pasco)
- 1 Dinamómetro de 10 N
- Masa de .
- Balanza digital
- Sistema base para colgar poleas
- Computador con programa Data Studio.
[edit] Procedimiento
- 1.- Arme el polipasto tal como aparece en la figura 3.
- 2.- Conecte en la parte inferior del sistema el sensor de fuerza Pasco.(ver figura 5)
3.- En el otro extremo de la cuerda ate un dinamómetro de , el cual medirá la fuerza externa aplicada al sistema. (ver figura 6)
4.- Encienda el computador y ejecute el programa Data Studio. Seleccione el Sensor de Fuerza.
5.- En el menú del programa, selecciones Opciones y active la opción de ingresar información por teclado. En este caso Ud. ingresará el valor que indica el dinamómetro.
6.- Una vez ajustado bien el dinamómetro al polipasto, comience a aumentar la fuerza externa (de a 1 N), registre el valor entregado por el dinamómetro seleccionando en el programa Keep e ingrese los valores a medida que vaya aumentando la fuerza.
[edit] Análisis
- 1.- En el mismo programa, obtenga el gráfico Fuerza sensor vs fuerza dinamómetro. Interprete físicamente el valor de la pendiente.
- 2.- Reemplace el sensor de Fuerza por una masa de
. En base al punto anterior calcule la masa que se necesita para levantar los 500 gr.
- 3.-¿Puede encontrar alguna relación entre la fuerza aplicada y el numero de poleas que conforman el polipasto para levantar una cierta masa?
- Encuentre el error experimental con respecto al teórico.
[edit] Experimento III: “ Cálculo de  ”
”
[edit] Objetivo
Obtener el valor de la aceleración de gravedad utilizando un sistema de poleas.
[edit] Introducción
En esta experiencia se utilizará una polea de dos pasos, la cual conforma el Sensor de movimiento Rotacional, con el cual se procederá a variar la masa del sistema y medir las variables del movimiento rotacional que permitirá comprobar el valor de .
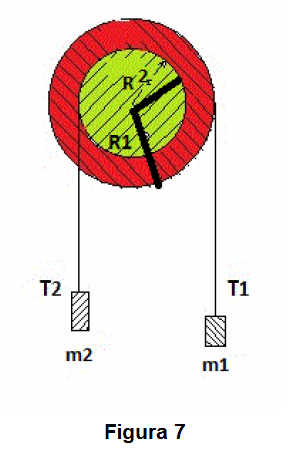
De la figura 7 se obtiene la ecuación del movimiento para el sistema:
donde,
siendo la masa de las poleas, y considerándola despreciable (
)
Luego
Para este sistema se tiene las siguientes ecuaciones de fuerzas:
Reemplazando (1) en (3), y considerando la restricción cinemática:
donde . Despejando
, se obtiene
[edit] Materiales
- Sensor de Movimiento Rotacional Pasco
- 2 trozos de hilo
- 2 ganchos con masas
- Balanza digital
- Sistema base para colgar poleas
- Computador con programa Data Studio.
[edit] Procedimiento
- 1.- Instale el Sensor de movimiento rotacional en la base metálica, y conéctelo a la interfaz. Asegúrese que el cable amarillo esté en el Canal A y el cable negro en el Canal B.
- 2.- Cuelgue los hilos en las poleas del sensor con las pesas y sus ganchos previamente masadas en la balanza. Ver Figura 8.
- 3.- Cuando amarre los hilos en las poleas, asegúrese que los nudos queden por detrás de ésta, para no trancar el movimiento.
- 4.- En el programa Data Studio seleccione el sensor rotacional. En el mismo icono de este sensor seleccione la medición que realizará el sensor, rapidez angular y la frecuencia de muestreo,
.
- 5.- En el programa presione Start, y en ese momento suelta el sistema, presione Stop cuando las pesas hayan terminado su recorrido.
- 6.- Obtenga el gráfico rapidez angular vs tiempo. Observe la curva obtenida y encuentre el mejor valor para la pendiente del gráfico. Para ello realice un ajuste lineal (incorporado en el programa).
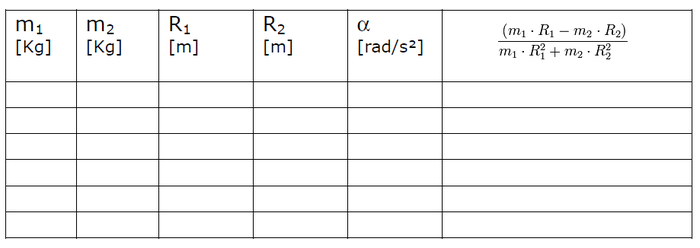
- 7.- Realice la experiencia nuevamente para 5 pares diferentes de masas colgantes. Repita el punto 6 para cada experiencia. Realice una tabla como la siguiente:
8.- Usando Excel, realice una gráfica de las aceleraciones angulares obtenidas en el punto versus
. Interprete físicamente el valor de la pendiente obtenida.