Ondas Estacionarias en 1-D (Fiz0312)

Revision as of 14:59, 11 July 2011

Ondas Estacionarias en 1-D

Objetivo

Estudiar ondas estacionarias en un medio 1-D

Introducción

El experimento coniste en el estudio de modos normales de vibración asociados a ondas estacionarias transversales y longitudeinales en un medio 1-D.

Los modos normales de vibración asociados a ondas estacionarias en un medio 1-D de largo L, con extremos fijos, tienen la forma:

$LaTeX: y_n(x,t)=A\sin(k_n x) \cdot \cos(\omega_n t)$

en el caso de ondas transversales, y

$LaTeX: s_n(x,t)=A\sin(k_n x) \cdot \cos(\omega_n t)$

Para el caso de ondas longitudinales.

En ambos casos,

$LaTeX: k_n=n \pi /L$

$LaTeX: \omega_n=n \pi v/L$

y $LaTeX: n=1,2,3,....$ , y $LaTeX: v$ es la velocidad de propagación de las ondas en el medio.

Procedimiento Experimental

Para ambos casis, ondas transversales y longitudinales, se usa el siguiente equipamiento:

- Amploficador de potencia PASCO CI-6502

- Computador PC con interfaz PASCO SCIENCE WORKSHOP

- Parlante.

- Programa DATA STUDIO.

Ondas Transversales

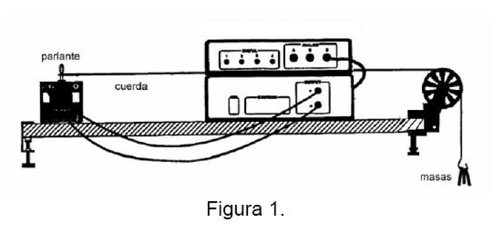
1. Las ondas son generadas en una cuerda excitada transversalmente por un parlante vibrando a frecuencia variable, como muestra la figura 1. La cuerda está unida por un extremo al centro del parlante, y tiene un gancho para agregar masas, generando una tensión variable en el extremo libre

2. La tensión de la cuerda se ajusta agregando golillas al gancho del extremo colgante. No agregue más de 12 golillas al gancho.

3. Mida la densidad lineal de masa de la cuerda.

4. Conecte el parlante al amplificador de potencia.

5. Conecte el amplificador de potencia de la interfaz PASCO.

6. Active el programa Data Studio.

7. En el programa seleccione Amplificador de Potencia y luego forma de onda AC Waveform. Luego de encendido el amplificador de potencia, selecciones $LaTeX: 5V$ (no más) para la amplitud de la señal, y una frecuencia inicial del orden de los $LaTeX: 20Hz$ .

8. Para distintos valores de la tensión de la cuerda, encuentre las frecuencias corrspondientes a los modos normales de vibración, caracterizados por el número $LaTeX: n$ correspondiente.

9. Usando gráficos de la forma $LaTeX: \omega$ $LaTeX: versus$ $LaTeX: n$ , determine para las distintas tensiones la velocidad de propagación de ondas transversales en la cuerda.

10. Analice gráficamente la relación entre la tensión de la cuerda y la velocidad de propagación de las ondas.

Ondas Longitudinales

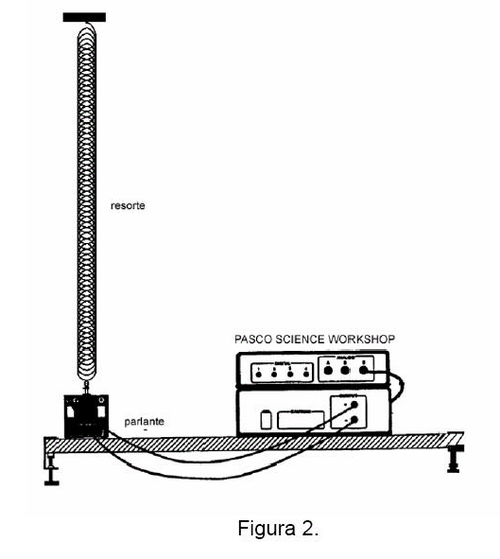
1. Las ondas son generadas en un resorte excitado longitudinalmente por un parlante vibrando a frecuencia variable, como muestra la figura 2. El resorte está unido por un extremo al centro del parlante y el otro extremo está fijo. La tensión del resorte se ajusta variando su largo extendido.

2. Determine la constante elástica del resorte.

3. Conecte el amplificador de potencia y la interfaz PASCO del mismo modo que en el caso de las ondas transversales en la cuerda. Mantenga el valor de voltaje en $LaTeX: 5V$ para la amplitud de oscilación.

4. Para distintos valores de la tensión del resorte, encuentre las frecuencias correspondientes a los modos normales de vibración, caracterizados por el número $LaTeX: n$ correspondiente.

5. Usando gráficos de la forma $LaTeX: \omega$ $LaTeX: versus$ $LaTeX: n$ , determine para las distintas tensiones la velocidad de propagación de ondas longitudinales en el resorte.

6. Analice gráficamente la relación entre la tensión del resorte y la velocidad de propagación de las ondas.

@@ Line 28: / Line 28: @@
 :<math>\omega_n=n \pi v/L</math>
- y <math>n=1,2,3,....</math>, y <math>v</math> es la velocidad de propagación de las ondas en el medio.
+y <math>n=1,2,3,....</math>, y <math>v</math> es la velocidad de propagación de las ondas en el medio.
 ===Procedimiento Experimental===

Ondas Estacionarias en 1-D (Fiz0312)

Revision as of 14:59, 11 July 2011

Contents