Dinámica de Oscilaciones (Fiz 121)
(→Introducción) |
|||
| (4 intermediate revisions by one user not shown) | |||
| Line 30: | Line 30: | ||
| − | :::<math>m\ddot{y}=mg - ky</math> |
+ | :::<m>m\ddot{y}=mg - ky</m> |
| − | donde <math>y</math> es medido desde el punto de equilibrio <math>y_0</math> en que la masa se encuentra en reposo sometida a la fuerza restauradora del resorte y el peso. La solución a la ecuación de movimiento está dada por, |
+ | donde <m>y</m> es medido desde el punto de equilibrio <m>y_0</m> en que la masa se encuentra en reposo sometida a la fuerza restauradora del resorte y el peso. La solución a la ecuación de movimiento está dada por, |
| − | :::<math>y(t)=A \cdot \sin(\omega_0 t)</math> |
+ | :::<m>y(t)=A \cdot \sin(\omega_0 t)</m> |
donde A es la amplitud de la oscilación y ω0 es la frecuencia de oscilación, dada por, |
donde A es la amplitud de la oscilación y ω0 es la frecuencia de oscilación, dada por, |
||
| − | :::<math>\omega_0 = \sqrt{\frac{k}{m}}</math> |
+ | :::<m>\omega_0 = \sqrt{\frac{k}{m}}</m> |
| − | y se ha elegido como condición inicial <math>y = 0</math> en <math>t = 0</math>. |
+ | y se ha elegido como condición inicial <m>y = 0</m> en <m>t = 0</m>. |
La energía mecánica del sistema está dada por la suma de los términos de energía cinética y energía potencia. |
La energía mecánica del sistema está dada por la suma de los términos de energía cinética y energía potencia. |
||
| − | :::<math>E=\frac{1}{2}mv^2+\frac{1}{2}ky^2</math> |
+ | :::<m>E=\frac{1}{2}mv^2+\frac{1}{2}ky^2</m> |
| Line 54: | Line 54: | ||
[[File:Reso2.png|right|thumb|300px| Figura 2]] |
[[File:Reso2.png|right|thumb|300px| Figura 2]] |
||
| − | :::<math>m \ddot{x} =− mg\frac{x}{l} −k(x − y )</math> |
+ | :::<m>m \ddot{x} =- mg\frac{x}{l} -k(x - y )</m> |
| − | :::<math>m \ddot{y} =− mg\frac{y}{l} + (x − y )</math> |
+ | :::<m>m \ddot{y} =- mg\frac{y}{l} + (x - y )</m> |
| − | donde <math>x</math> e <math>y</math> está medidos respecto de la posición de equilibrio de la masa respectiva y se ha supuesto que las masas y largos de cuerdas de los péndulos son idénticas. |
+ | donde <m>x</m> e <m>y</m> está medidos respecto de la posición de equilibrio de la masa respectiva y se ha supuesto que las masas y largos de cuerdas de los péndulos son idénticas. |
| − | Introduciendo <math>\omega_0=\sqrt{g/l}</math> como frecuencia natural de oscilación de cada péndulo aislado, el sistema de ecuaciones puede escribirse como |
+ | Introduciendo <m>\omega_0=\sqrt{g/l}</m> como frecuencia natural de oscilación de cada péndulo aislado, el sistema de ecuaciones puede escribirse como |
| − | :::<math>\ddot{x} + \omega_0 ^2x =−\frac{k}{m}(x − y )</math> |
+ | :::<m>\ddot{x} + \omega_0 ^2x =-\frac{k}{m}(x - y )</m> |
| − | :::<math>m \ddot{y} + \omega_0 ^2y =\frac{k}{m}(x − y )</math> |
+ | :::<m>m \ddot{y} + \omega_0 ^2y =\frac{k}{m}(x - y )</m> |
| − | Para encontrar la solución al sistema de ecuaciones se introducen variables auxiliares <math>X</math> e <math>Y</math>, definidas como, |
+ | Para encontrar la solución al sistema de ecuaciones se introducen variables auxiliares <m>X</m> e <m>Y</m>, definidas como, |
| − | :::<math>X=(x+y)</math> |
+ | :::<m>X=(x+y)</m> |
| − | :::<math>Y=(x-y)</math> |
+ | :::<m>Y=(x-y)</m> |
Sumando y restando las ecuaciones originales y usando las nuevas variables, se obtienen las ecuaciones independientes |
Sumando y restando las ecuaciones originales y usando las nuevas variables, se obtienen las ecuaciones independientes |
||
| − | :::<math>\ddot{X}+\omega_0^2 X=0</math> |
+ | :::<m>\ddot{X}+\omega_0^2 X=0</m> |
| − | :::<math>\ddot{Y}+\left(\omega_0^2+\frac{2k}{m}\right) Y=0</math> |
+ | :::<m>\ddot{Y}+\left(\omega_0^2+\frac{2k}{m}\right) Y=0</m> |
| Line 89: | Line 89: | ||
Las soluciones de estas ecuaciones escritas en términos de las nuevas coordenadas implican que el sistema físico tiene dos frecuencias naturales de oscilación, |
Las soluciones de estas ecuaciones escritas en términos de las nuevas coordenadas implican que el sistema físico tiene dos frecuencias naturales de oscilación, |
||
| − | :::<math>\omega_1=\omega_0=\sqrt{\frac{g}{l}}</math> |
+ | :::<m>\omega_1=\omega_0=\sqrt{\frac{g}{l}}</m> |
| − | :::<math>\omega_2=\sqrt{\left(\omega_0^2+\frac{2k}{m}\right)}=\sqrt{\left(\frac{g}{l}+\frac{2k}{m}\right)}</math> |
+ | :::<m>\omega_2=\sqrt{\left(\omega_0^2+\frac{2k}{m}\right)}=\sqrt{\left(\frac{g}{l}+\frac{2k}{m}\right)}</m> |
| − | Si la oscilación ocurre en fase, esto es, <math>x = y</math>, la dinámica está determinada por la ecuación para <math>X</math> y la frecuencia de oscilación de ambas masas es <math>\omega_1</math>. Si, en cambio, la oscilación ocurre en antifase, es decir, <math>x = -y</math>, la dinámica está descrita por la ecuación para <math>Y</math> y la frecuencia de oscilación es <math>\omega_2</math>. |
+ | Si la oscilación ocurre en fase, esto es, <m>x = y</m>, la dinámica está determinada por la ecuación para <m>X</m> y la frecuencia de oscilación de ambas masas es <m>\omega_1</m>. Si, en cambio, la oscilación ocurre en antifase, es decir, <m>x = -y</m>, la dinámica está descrita por la ecuación para <m>Y</m> y la frecuencia de oscilación es <m>\omega_2</m>. |
En general la oscilación ocurre en una combinación de ambos modos de oscilación. En este caso las expresiones que describen la dinámica del sistema son, |
En general la oscilación ocurre en una combinación de ambos modos de oscilación. En este caso las expresiones que describen la dinámica del sistema son, |
||
| − | :::<math>X (t ) = x(t) + y (t) = X_0 \cdot \sin(\omega_1t + \phi_1 )</math> |
+ | :::<m>X (t ) = x(t) + y (t) = X_0 \cdot \sin(\omega_1t + \phi_1 )</m> |
| − | :::<math>Y (t ) = x(t ) − y (t ) = Y_0 \cdot \sin(\omega_2 t + \phi_2 )</math> |
+ | :::<m>Y (t ) = x(t ) - y (t ) = Y_0 \cdot \sin(\omega_2 t + \phi_2 )</m> |
A partir de estas expresiones se puede obtener para la oscilación individual de cada masa, |
A partir de estas expresiones se puede obtener para la oscilación individual de cada masa, |
||
| − | :::<math>x(t ) = \frac{1}{2}( X_0 \cdot \sin(\omega_1t + \phi_1 ) + Y_0 \sin(\omega_2 t + \phi_2 ))</math> |
+ | :::<m>x(t ) = \frac{1}{2}( X_0 \cdot \sin(\omega_1t + \phi_1 ) + Y_0 \sin(\omega_2 t + \phi_2 ))</m> |
| − | :::<math>y (t ) = ( X_0 \cdot \sin(\omega_1t + \phi_1 ) − Y_0 \sin(\omega_2 t + \phi_2 ))</math> |
+ | :::<m>y (t ) = ( X_0 \cdot \sin(\omega_1t + \phi_1 ) - Y_0 \sin(\omega_2 t + \phi_2 ))</m> |
| − | Para el caso particular en que <math>X_0 = Y_0 = 2A</math> y <math>\phi_1 = \phi_2 = 0</math>, se obtiene, |
+ | Para el caso particular en que <m>X_0 = Y_0 = 2A</m> y <m>\phi_1 = \phi_2 = 0</m>, se obtiene, |
| − | :::<math>x(t)=2A\cos \left(\frac{\omega_1 - \omega_2}{2}t\right) \cdot \sin\left(\frac{\omega_1 + \omega_2}{2}t\right) </math> |
+ | :::<m>x(t)=2A\cos \left(\frac{\omega_1 - \omega_2}{2}t\right) \cdot \sin\left(\frac{\omega_1 + \omega_2}{2}t\right) </m> |
| − | :::<math>y(t)=2A\cos \left(\frac{\omega_1 + \omega_2}{2}t\right) \cdot \sin\left(\frac{\omega_1 - \omega_2}{2}t\right)=2A\cos \left(\frac{\omega_1 - \omega_2}{2}t+\frac{\pi}{2}\right) \cdot \sin\left(\frac{\omega_1 + \omega_2}{2}t + \frac{\pi}{2}\right)</math> |
+ | :::<m>y(t)=2A\cos \left(\frac{\omega_1 + \omega_2}{2}t\right) \cdot \sin\left(\frac{\omega_1 - \omega_2}{2}t\right)=2A\cos \left(\frac{\omega_1 - \omega_2}{2}t+\frac{\pi}{2}\right) \cdot \sin\left(\frac{\omega_1 + \omega_2}{2}t + \frac{\pi}{2}\right)</m> |
| Line 121: | Line 121: | ||
| − | :::<math>E = \frac{1}{2}k (l_0 − ( y − x ))^2 + \frac{1}{2}mv_1^2 + \frac{1}{2}mv_2^2</math> |
+ | :::<m>E = \frac{1}{2}k (l_0 - ( y - x ))^2 + \frac{1}{2}mv_1^2 + \frac{1}{2}mv_2^2</m> |
| − | donde <math>l_0</math> es la longitud del resorte en equilibrio y <math>v_1</math>, <math>v_2</math> son las velocidades de las masas. |
+ | donde <m>l_0</m> es la longitud del resorte en equilibrio y <m>v_1</m>, <m>v_2</m> son las velocidades de las masas. |
=== Montaje Experimental === |
=== Montaje Experimental === |
||
| Line 173: | Line 173: | ||
==== <u>Experimento B)</u> ==== |
==== <u>Experimento B)</u> ==== |
||
| − | : a) Para cada una de las mediciones realizadas genere gráficos que muestren en sus experimentos la evolución temporal la amplitud de oscilación de ambas masas y de las coordenadas generalizadas <math>X</math> e <math>Y</math>, introducidas en el modelo teórico. |
+ | : a) Para cada una de las mediciones realizadas genere gráficos que muestren en sus experimentos la evolución temporal la amplitud de oscilación de ambas masas y de las coordenadas generalizadas <m>X</m> e <m>Y</m>, introducidas en el modelo teórico. |
| − | : b) A partir de los gráficos anteriores determine las frecuencias características <math>\omega_1</math> y <math>\omega_2</math>, y compare con los valores que predice el modelo teórico. |
+ | : b) A partir de los gráficos anteriores determine las frecuencias características <m>\omega_1</m> y <m>\omega_2</m>, y compare con los valores que predice el modelo teórico. |
: c) Genere en cada caso gráficos para las energías cinética, potencial y mecánica total del sistema. |
: c) Genere en cada caso gráficos para las energías cinética, potencial y mecánica total del sistema. |
||
Latest revision as of 07:20, 29 October 2014
Contents |
[edit] Dinámica de Oscilaciones
[edit] Objetivo
Estudiar la dinámica de objetos que experimental movimiento oscilatorio armónico.
[edit] Materiales
- Cámara VideoCom
- Computador con programa VideoCom Movimiento
- Masas
- Péndulos
- Resortes
- Balanza
- Programa para procesamiento de datos.
[edit] Introducción
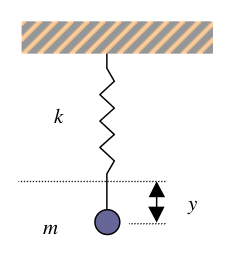
De acuerdo con el esquema de la figura 1, al oscilar la masa a lo largo de la vertical, la ecuación de movimiento es,
donde es medido desde el punto de equilibrio
en que la masa se encuentra en reposo sometida a la fuerza restauradora del resorte y el peso. La solución a la ecuación de movimiento está dada por,
donde A es la amplitud de la oscilación y ω0 es la frecuencia de oscilación, dada por,
y se ha elegido como condición inicial en
.
La energía mecánica del sistema está dada por la suma de los términos de energía cinética y energía potencia.
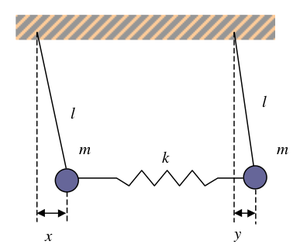
De acuerdo con el esquema de la figura 2, al oscilar las masa a lo largo de la horizontal, las respectivas ecuaciones de movimiento están dadas por
donde e
está medidos respecto de la posición de equilibrio de la masa respectiva y se ha supuesto que las masas y largos de cuerdas de los péndulos son idénticas.
Introduciendo como frecuencia natural de oscilación de cada péndulo aislado, el sistema de ecuaciones puede escribirse como
Para encontrar la solución al sistema de ecuaciones se introducen variables auxiliares e
, definidas como,
Sumando y restando las ecuaciones originales y usando las nuevas variables, se obtienen las ecuaciones independientes
Las soluciones de estas ecuaciones escritas en términos de las nuevas coordenadas implican que el sistema físico tiene dos frecuencias naturales de oscilación,
Si la oscilación ocurre en fase, esto es, , la dinámica está determinada por la ecuación para
y la frecuencia de oscilación de ambas masas es
. Si, en cambio, la oscilación ocurre en antifase, es decir,
, la dinámica está descrita por la ecuación para
y la frecuencia de oscilación es
.
En general la oscilación ocurre en una combinación de ambos modos de oscilación. En este caso las expresiones que describen la dinámica del sistema son,
A partir de estas expresiones se puede obtener para la oscilación individual de cada masa,
Para el caso particular en que y
, se obtiene,
La energía mecánica del sistema, suponiendo que la oscilación es puramente a lo largo de la horizontal, está dada por,
donde es la longitud del resorte en equilibrio y
,
son las velocidades de las masas.
[edit] Montaje Experimental
[edit] Procedimiento
En este laboratorio se desarrollarán dos experimentos:
- 1. Dinámica de oscilación de una masa unida a un resorte, a lo largo de la vertical
- 2. Dinámica de oscilación de dos péndulos acoplados por un resorte, a lo largo de la horizontal.
Para el procesamiento cuantitativo de sus datos experimentales necesario conocer las masas involucradas, la constante elástica del resorte, su longitud y los largos de péndulos.. Para el montaje A) siga el siguiente procedimiento:
- Para un valor dado de la masa unida al resorte, elegida de modo tal que el resorte experimente en reposo un estiramiento moderado, registre el movimiento oscilatorio a lo largo de la vertical.
- Repita la medición anterior para un par de valores adicionales de la masa.
Para el montaje B) siga el procedimiento siguiente:
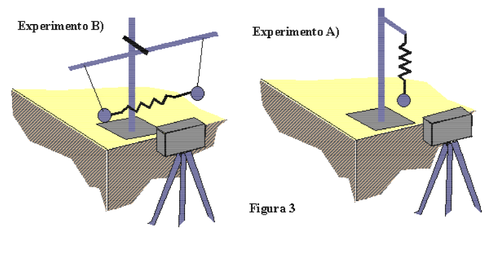
- Construya el sistema de péndulos acoplados por un resorte, como muestra la figura 3. Cuide que las masas sean lo más iguales posibles y que el largo de los péndulos sea el
mismo.
- Con el sistema en reposo mida cuidadosamente la longitud del resorte en equilibrio y el
largo de los péndulos.
- Ponga los péndulos a oscilar en fase, esto es, en la misma dirección, y registre el movimiento de las masas durante un tiempo suficiente como para que se observen varios períodos de oscilación de las mismas.
- Ponga los péndulos a oscilar en contrafase, esto es, en direcciones opuestas, y registre el movimiento de las masas durante un tiempo suficiente como para que se observen varios períodos de oscilación de las mismas.
- Ponga los péndulos a oscilar de manera arbitraria, cuidando que la oscilación sea a lo largo de una línea en dirección horizontal, y registre el movimiento de las masas durante un tiempo suficiente como para que se observen varios períodos de oscilación de las mismas.
[edit] Análisis
Obtenidos los datos experimentales, realice el siguiente proceso de análisis:
[edit] Experimento A)
- a) Determine experimentalmente la frecuencia de oscilación de la masa y compare con el valor que predice el modelo teórico.
- b) Genere gráficos que muestren la evolución temporal de la energía cinética, energía potencia y energía mecánica total del sistema.
- c) A partir de los gráficos obtenidos, discuta la conservación de la energía mecánica en su sistema.
[edit] Experimento B)
- a) Para cada una de las mediciones realizadas genere gráficos que muestren en sus experimentos la evolución temporal la amplitud de oscilación de ambas masas y de las coordenadas generalizadas
e
, introducidas en el modelo teórico.
- b) A partir de los gráficos anteriores determine las frecuencias características
y
, y compare con los valores que predice el modelo teórico.
- c) Genere en cada caso gráficos para las energías cinética, potencial y mecánica total del sistema.
- d) A partir de los gráficos obtenidos, discuta la conservación de energía mecánica en su sistema.