Estática (Fis 151/Fis 1513)
(→Montaje Experimental y procedimiento:) |
|||
| Line 18: | Line 18: | ||
| − | <center><math>\sum \vec{F_{ext}} = \vec{0} \qquad \qquad \qquad (1)</math></center> |
+ | <center><m>\sum \vec{F_{ext}} = \vec{0} \qquad \qquad \qquad (1)</m></center> |
| − | <center><math>\sum \vec{\tau_{ext}} = \vec{0} \qquad \qquad \qquad (2)</math></center> |
+ | <center><m>\sum \vec{\tau_{ext}} = \vec{0} \qquad \qquad \qquad (2)</m></center> |
| Line 30: | Line 30: | ||
Antes de comenzar la experiencia, es conveniente hacer un análisis teórico del problema en cuestión. |
Antes de comenzar la experiencia, es conveniente hacer un análisis teórico del problema en cuestión. |
||
| − | Para simplificar el análisis supondremos que las masas de los elementos del puente son despreciables. En el experimento se colgará una masa desde la viga central. En el diagrama del cuerpo libre de la Figura 2, la fuerza correspondiente al peso de esta masa está representada por <math>\vec{P}</math>. |
+ | Para simplificar el análisis supondremos que las masas de los elementos del puente son despreciables. En el experimento se colgará una masa desde la viga central. En el diagrama del cuerpo libre de la Figura 2, la fuerza correspondiente al peso de esta masa está representada por <m>\vec{P}</m>. |
| − | Según la notación que hemos adoptado, los subíndices de las fuerzas se corresponden con las estructuras involucradas, por ejemplo <math>\vec{F_{AB}}</math> es la fuerza ejercida por la estructura AB sobre el soporte A. |
+ | Según la notación que hemos adoptado, los subíndices de las fuerzas se corresponden con las estructuras involucradas, por ejemplo <m>\vec{F_{AB}}</m> es la fuerza ejercida por la estructura AB sobre el soporte A. |
| Line 46: | Line 46: | ||
| − | <center><math>N_A + N_E - \frac{P}{2} = 0 \qquad \qquad \qquad (3)</math></center> |
+ | <center><m>N_A + N_E - \frac{P}{2} = 0 \qquad \qquad \qquad (3)</m></center> |
| − | donde, <math>N_A</math> y <math>N_E</math> son las normales en los pernos A y E respectivamente. |
+ | donde, <m>N_A</m> y <m>N_E</m> son las normales en los pernos A y E respectivamente. |
Notemos que las fuerzas internas no entran en el análisis. Dada la simetría del problema obtenemos directamente que, |
Notemos que las fuerzas internas no entran en el análisis. Dada la simetría del problema obtenemos directamente que, |
||
| − | :<center><math>N_A = N_E =- \frac{P}{2} \qquad \qquad \qquad (4)</math></center> |
+ | :<center><m>N_A = N_E =- \frac{P}{2} \qquad \qquad \qquad (4)</m></center> |
| Line 61: | Line 61: | ||
| − | :<center><math>F_{AB} = \frac{N_A}{\sin(\theta)} = \frac{P}{2 \cdot \sin(\theta)}</math></center> |
+ | :<center><m>F_{AB} = \frac{N_A}{\sin(\theta)} = \frac{P}{2 \cdot \sin(\theta)}</m></center> |
| − | :<center><math>F_{CA} = F_{AB} \cdot \cos(\theta) = \frac{P}{2} \cdot \mathrm{cotg}(\theta)</math></center> |
+ | :<center><m>F_{CA} = F_{AB} \cdot \cos(\theta) = \frac{P}{2} \cdot \mathrm{cotg}(\theta)</m></center> |
| − | :<center><math>F_{BC} = \frac{P}{2 \cdot \sin (\theta)}</math></center> |
+ | :<center><m>F_{BC} = \frac{P}{2 \cdot \sin (\theta)}</m></center> |
| − | :<center><math>F_{BD} =(F_{AB} + F_{BC}) \cdot \cos(\theta) = P \cdot \mathrm{cotg}(\theta)</math></center> |
+ | :<center><m>F_{BD} =(F_{AB} + F_{BC}) \cdot \cos(\theta) = P \cdot \mathrm{cotg}(\theta)</m></center> |
| − | donde <math>\theta</math>, es el ángulo que forman las barras con la horizontal (ver Figura 2). |
+ | donde <m>\theta</m>, es el ángulo que forman las barras con la horizontal (ver Figura 2). |
Latest revision as of 06:38, 29 October 2014
Contents |
[edit] Estática
[edit] Objetivos
- Estudiar las condiciones de equilibrio.
- Medir experimentalmente las tensiones en un puente reticulado.
[edit] Introducción
La estática es la parte de la física que estudia los sistemas bajo la acción de fuerzas y torques que se equilibran. Bajo estas condiciones un cuerpo está en reposo permanecerá en ese estado y decimos que se encuentra en equilibrio estático.
Para que una partícula esté en equilibrio estático es necesario que la suma de todas las fuerzas que actúan sobre ella sea cero. De manera similar, para que un cuerpo rígido permanezca en reposo la fuerza neta sobre su centro de masas (CM) debe ser cero, sin embargo, esta condición no es suficiente para el equilibrio estático pues el cuerpo también podría rotar. En este caso, para que el equilibrio estático exista, el torque neto de que actúa sobre el cuerpo también debe ser cero.
Resumiendo, las condiciones para el equilibrio estático son:
[edit] Experimento
En este experimento mediremos las tensiones aplicadas sobre las vigas de una estructura tipo puente reticulado que se muestra en la Figura 1.
Antes de comenzar la experiencia, es conveniente hacer un análisis teórico del problema en cuestión.
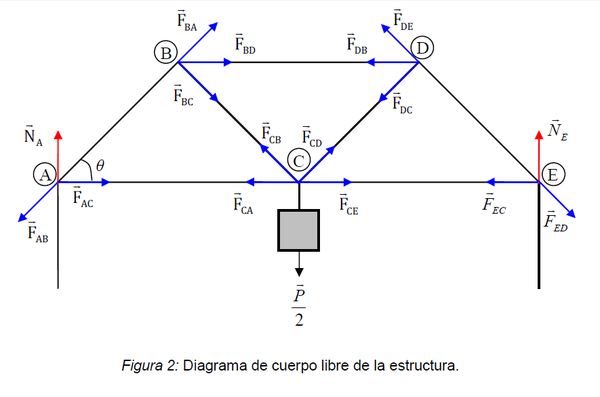
Para simplificar el análisis supondremos que las masas de los elementos del puente son despreciables. En el experimento se colgará una masa desde la viga central. En el diagrama del cuerpo libre de la Figura 2, la fuerza correspondiente al peso de esta masa está representada por .
Según la notación que hemos adoptado, los subíndices de las fuerzas se corresponden con las estructuras involucradas, por ejemplo es la fuerza ejercida por la estructura AB sobre el soporte A.
Para determinar la fuerza en las barras aplicamos las condiciones de equilibrio estático.
De la ecuación (1) obtenemos:
donde, y
son las normales en los pernos A y E respectivamente.
Notemos que las fuerzas internas no entran en el análisis. Dada la simetría del problema obtenemos directamente que,
Las fuerzas que actúan en cada soporte se calculan de las condiciones de equilibrio en cada punto, así obtenemos:
donde , es el ángulo que forman las barras con la horizontal (ver Figura 2).
[edit] Equipamiento
- Balanza.
- 4 celdas de carga.
- Colgador de masas.
- Componentes para armar el puente.
- Computadora con Interfaz Science Workshop Pasco.
[edit] Montaje Experimental y procedimiento:
- Monte el puente que se muestra en la Figura 1. (Tenga especial cuidado con no dañar las celdas de carga.)
- Conecte en forma ordenada las celdas a la interfaz Pasco.
- En su computador despliegue gráficos, de manera que pueda ver las mediciones de todas las celdas de carga.
- Mida las fuerzas de tensión o compresión en las celdas para cuatro masas diferentes colgadas desde la viga central. En cada medición inmediatamente antes de colgar la masa, usted debe presionar el botón “tar” de la interfaz. Al presionar este botón, los valores de las fuerzas medidas por las celdas en ese instante serán tomadas como el valor “cero”. ¿Por qué es conveniente hacer esto? Explique.
- Haga un gráfico de las fuerzas medidas en función del peso aplicado.¿Qué representa el signo de cada una de las fuerzas medidas? Compare sus resultados con el cálculo que mostrado anteriormente. Explique.