Circuito RLC (Fiz0221)
From Uv
(Difference between revisions)
(→Circuito RLC) |
|||
| (2 intermediate revisions by one user not shown) | |||
| Line 7: | Line 7: | ||
=== Teoría === |
=== Teoría === |
||
| − | La amplitud de la corriente AC(<math>I_0</math>) en un circuito en serie RLC depende de la amplitud del voltaje aplicado(<math>V_0</math>) y la impedancia (<math>Z</math>). Lo anterior queda expresado como: |
+ | La amplitud de la corriente AC(<m>I_0</m>) en un circuito en serie RLC depende de la amplitud del voltaje aplicado(<m>V_0</m>) y la impedancia (<m>Z</m>). Lo anterior queda expresado como: |
| − | :<math>I_0= \frac{V_0}{Z}</math> (1) |
+ | :<center><m>I_0= \frac{V_0}{Z} \qquad\qquad\qquad (1)</m></center> |
Ya que la impedancia depende de la frecuencia, entonces la corriente varía con la frecuencia de la siguiente forma: |
Ya que la impedancia depende de la frecuencia, entonces la corriente varía con la frecuencia de la siguiente forma: |
||
| − | :<math>Z=\sqrt{(X_L-X_C)^2+R^2}</math> (2) |
+ | :<center><m>Z=\sqrt{(X_L-X_C)^2+R^2} \qquad\qquad\qquad (2)</m></center> |
donde: |
donde: |
||
| − | <math>X_L</math> = reactancia inductiva |
+ | <m>X_L</m> = reactancia inductiva |
| − | <math>X_C</math> = reactancia capacitiva |
+ | <m>X_C</m> = reactancia capacitiva |
| − | <math>R</math> = resistencia |
+ | <m>R</m> = resistencia |
| − | <math>\omega</math> =frecuencia angular |
+ | <m>\omega</m> =frecuencia angular |
| − | <math>X_L = \omega L</math> |
+ | <m>X_L = \omega L</m> |
| − | <math>X_C = 1/\omega C</math> |
+ | <m>X_C = 1/\omega C</m> |
| − | <math>\omega = 2 \pi \nu</math>, (siendo <math>\nu</math> la frecuencia lineal) |
+ | <m>\omega = 2 \pi \nu</m>, (siendo <m>\nu</m> la frecuencia lineal) |
La corriente será máxima cuando el circuito sea dirigido a una frecuencia de resonancia: |
La corriente será máxima cuando el circuito sea dirigido a una frecuencia de resonancia: |
||
| − | :<math>\omega_{res}=\frac{1}{\sqrt{LC}}</math> (3) |
+ | :<center><m>\omega_{res}=\frac{1}{\sqrt{LC}} \qquad\qquad\qquad (3)</m></center> |
| − | sabiendo que <math>\omega_{res}= 2 \pi f</math>, |
+ | sabiendo que <m>\omega_{res}= 2 \pi f</m>, |
| − | :<math>f_{res}=\frac{1}{2 \pi \sqrt{LC}}</math> (4) |
+ | :<center><m>f_{res}=\frac{1}{2 \pi \sqrt{LC}} \qquad\qquad\qquad (4)</m></center> |
| − | Se puede demostrar que en resonancia <math>X_L = X_C</math> y entonces la impedancia será igual a <math>R</math>. En resonancia, la impedancia tiene el valor mas bajo posible y la corriente tiene el valor mas alto. |
+ | Se puede demostrar que en resonancia <m>X_L = X_C</m> y entonces la impedancia será igual a <m>R</m>. En resonancia, la impedancia tiene el valor mas bajo posible y la corriente tiene el valor mas alto. |
| Line 52: | Line 52: | ||
| − | ::* Deberá determinar la amplitud de la corriente a través de la resistencia y dibujar corriente <math>versus</math> frecuencia. |
+ | ::* Deberá determinar la amplitud de la corriente a través de la resistencia y dibujar corriente <m>versus</m> frecuencia. |
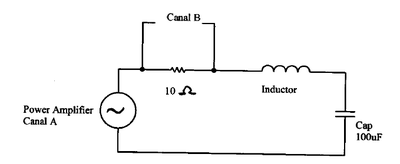
: a) Arme el circuito RLC serie como lo indica la figura 1, y conéctelo al amplificador de potencia Pasco. |
: a) Arme el circuito RLC serie como lo indica la figura 1, y conéctelo al amplificador de potencia Pasco. |
||
| Line 58: | Line 58: | ||
[[File:Rlc1.png|center|thumb|400px| Figura 1: Circuito experimental.]] |
[[File:Rlc1.png|center|thumb|400px| Figura 1: Circuito experimental.]] |
||
| − | : b) Compruebe con un capacitometro la capacidad del condensador. Conocido ya el valor de la inductancia <math>L</math> y medida la capacidad del condensador con un Capacitómetro, estime el valor de la frecuencia de resonancia. |
+ | : b) Compruebe con un capacitometro la capacidad del condensador. Conocido ya el valor de la inductancia <m>L</m> y medida la capacidad del condensador con un Capacitómetro, estime el valor de la frecuencia de resonancia. |
: c) Ejecute el programa ''Data Studio''. |
: c) Ejecute el programa ''Data Studio''. |
||
| − | : d) En el icono del sensor de voltaje seleccione '''Frecuencia de Muestreo''' a <math>1000hz</math>. |
+ | : d) En el icono del sensor de voltaje seleccione '''Frecuencia de Muestreo''' a <m>1000hz</m>. |
| − | : e) En el generador de señales, seleccione <math>3V</math> en amplitud , <math>10 Hz</math> en frecuencia y '''onda sinusoidal'''. |
+ | : e) En el generador de señales, seleccione <m>3V</m> en amplitud , <m>10 Hz</m> en frecuencia y '''onda sinusoidal'''. |
=== Procedimiento === |
=== Procedimiento === |
||
| Line 70: | Line 70: | ||
: 1) Encienda el amplificador de potencia. Presione Inicio para comenzar registrar los datos. El generador de señales comenzará automáticamente. |
: 1) Encienda el amplificador de potencia. Presione Inicio para comenzar registrar los datos. El generador de señales comenzará automáticamente. |
||
| − | : 2) En el osciloscopio presione '''smart cursor''' [[File:Bopton3.png|alt=Negrita|link=]], y muévalo a través de los peak de la curva del voltaje a través de la resistencia, <math>V_R</math> (media traza). Registre el voltaje para el canal B. |
+ | : 2) En el osciloscopio presione '''smart cursor''' [[File:Bopton3.png|alt=Negrita|link=]], y muévalo a través de los peak de la curva del voltaje a través de la resistencia, <m>V_R</m> (media traza). Registre el voltaje para el canal B. |
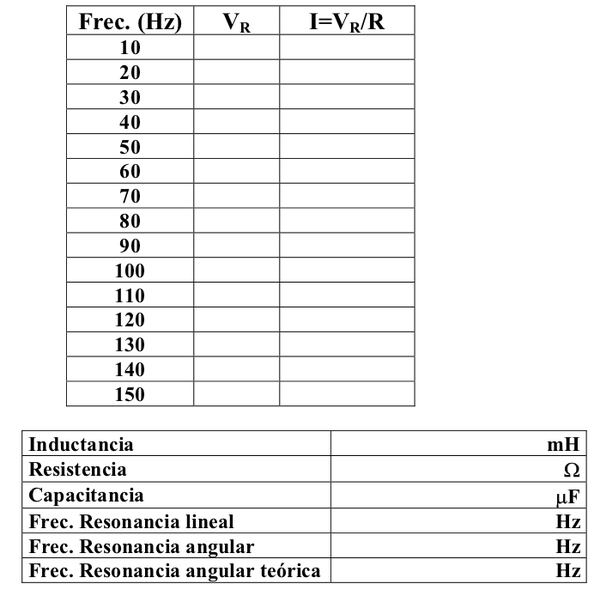
| − | : 3) En la ventana '''Generador de Señales''' aumente la frecuencia en <math>10 Hz</math>. En la Tabla de datos adjunta , registre el voltaje <math>V_R</math> para esta nueva frecuencia. |
+ | : 3) En la ventana '''Generador de Señales''' aumente la frecuencia en <m>10 Hz</m>. En la Tabla de datos adjunta , registre el voltaje <m>V_R</m> para esta nueva frecuencia. |
| − | : 4) Repita el proceso hasta que alcance los <math>50 Hz</math>. A esta frecuencia active el osciloscopio. Ajuste la velocidad de barrido de <math>1000 sampleos/seg</math> a <math>5000 sampleos/seg</math>. Encuentre el valor para <math>V_R</math> a esta frecuencia. |
+ | : 4) Repita el proceso hasta que alcance los <m>50 Hz</m>. A esta frecuencia active el osciloscopio. Ajuste la velocidad de barrido de <m>1000 sampleos/seg</m> a <m>5000 sampleos/seg</m>. Encuentre el valor para <m>V_R</m> a esta frecuencia. |
| − | : 5) Active la ventana del '''Generador de Señales'''. Aumente la frecuencia a <math>60 Hz</math>. Encuentre el nuevo valor de <math>V_R</math> para esta frecuencia. |
+ | : 5) Active la ventana del '''Generador de Señales'''. Aumente la frecuencia a <m>60 Hz</m>. Encuentre el nuevo valor de <m>V_R</m> para esta frecuencia. |
| − | : 6) Incremente la frecuencia en <math> 10 Hz</math> y repita el proceso hasta llegar a <math>150 Hz</math>. |
+ | : 6) Incremente la frecuencia en <m> 10 Hz</m> y repita el proceso hasta llegar a <m>150 Hz</m>. |
: 7) A partir de la tabla de datos determine la frecuencia de resonancia (donde el voltaje a través de la resistencia alcanza el valor máximo y el voltaje de salida con el voltaje de la resistencia está, en fase). |
: 7) A partir de la tabla de datos determine la frecuencia de resonancia (donde el voltaje a través de la resistencia alcanza el valor máximo y el voltaje de salida con el voltaje de la resistencia está, en fase). |
||
| Line 88: | Line 88: | ||
:: 1.- Calcule la corriente que circula a través de la resistencia y registre los valores obtenidos en la tabla de datos. |
:: 1.- Calcule la corriente que circula a través de la resistencia y registre los valores obtenidos en la tabla de datos. |
||
| − | :: 2.- Haga un gráfico Corriente <math>versus</math> Frecuencia Lineal. |
+ | :: 2.- Haga un gráfico Corriente <m>versus</m> Frecuencia Lineal. |
:: 3.- Usando el valor de la frecuencia de resonancia (obtenida del osciloscopio), calcule la frecuencia de resonancia angular y registre el valor en la tabla de datos. |
:: 3.- Usando el valor de la frecuencia de resonancia (obtenida del osciloscopio), calcule la frecuencia de resonancia angular y registre el valor en la tabla de datos. |
||
| Line 104: | Line 104: | ||
* ¿Cuál es el porcentaje de diferencia entre la frecuencia de resonancia angular medida con el valor teórico?. |
* ¿Cuál es el porcentaje de diferencia entre la frecuencia de resonancia angular medida con el valor teórico?. |
||
| − | * ¿Es la curva corriente <math>versus</math> frecuencia simétrica acerca de la frecuencia de resonancia?. Explique. |
+ | * ¿Es la curva corriente <m>versus</m> frecuencia simétrica acerca de la frecuencia de resonancia?. Explique. |
| − | * En resonancia, las reactancias del inductor y del capacitor se cancelan las unas a las otras por lo que la impedancia (<math>Z</math>) es igual a la resistencia ( <math>R</math> ). Calcule la resistencia del circuito usando la amplitud de la corriente en resonancia en la ecuación <math>R=V/I</math> (donde <math>V</math> es la amplitud del voltaje aplicado) ¿Es ésta resistencia igual a <math>10 \Omega</math>?.Explique. |
+ | * En resonancia, las reactancias del inductor y del capacitor se cancelan las unas a las otras por lo que la impedancia (<m>Z</m>) es igual a la resistencia ( <m>R</m> ). Calcule la resistencia del circuito usando la amplitud de la corriente en resonancia en la ecuación <m>R=V/I</m> (donde <m>V</m> es la amplitud del voltaje aplicado) ¿Es ésta resistencia igual a <m>10 \Omega</m>?.Explique. |
Latest revision as of 08:40, 28 October 2014
Contents |
[edit] Circuito RLC
[edit] Objetivo
Estudiar la resonancia de un circuito RLC, examinando la corriente a través del circuito como función de la frecuencia del voltaje aplicado.
[edit] Teoría
La amplitud de la corriente AC() en un circuito en serie RLC depende de la amplitud del voltaje aplicado(
) y la impedancia (
). Lo anterior queda expresado como:
Ya que la impedancia depende de la frecuencia, entonces la corriente varía con la frecuencia de la siguiente forma:
donde:
= reactancia inductiva
= reactancia capacitiva
= resistencia
=frecuencia angular
, (siendo
la frecuencia lineal)
La corriente será máxima cuando el circuito sea dirigido a una frecuencia de resonancia:
sabiendo que ,
Se puede demostrar que en resonancia y entonces la impedancia será igual a
. En resonancia, la impedancia tiene el valor mas bajo posible y la corriente tiene el valor mas alto.
[edit] Montaje
En esta actividad el amplificador de potencia produce una corriente alterna a través del circuito RLC. La amplitud de la corriente depende de la impedancia en el circuito, el cual varía con la frecuencia. El generador de señales controla la frecuencia. El sensor de voltaje mide la diferencia de potencial a través de la resistencia en el circuito.
Ud. usará el generador de señales para cambiar la frecuencia de voltaje aplicado.
- Deberá investigar la fase que relaciona el voltaje aplicado y el voltaje de la resistencia, así como varía la frecuencia.
- Deberá determinar la amplitud de la corriente a través de la resistencia y dibujar corriente
frecuencia.
- Deberá determinar la amplitud de la corriente a través de la resistencia y dibujar corriente
- a) Arme el circuito RLC serie como lo indica la figura 1, y conéctelo al amplificador de potencia Pasco.
- b) Compruebe con un capacitometro la capacidad del condensador. Conocido ya el valor de la inductancia
y medida la capacidad del condensador con un Capacitómetro, estime el valor de la frecuencia de resonancia.
- c) Ejecute el programa Data Studio.
- d) En el icono del sensor de voltaje seleccione Frecuencia de Muestreo a
.
- e) En el generador de señales, seleccione
en amplitud ,
en frecuencia y onda sinusoidal.
[edit] Procedimiento
- 1) Encienda el amplificador de potencia. Presione Inicio para comenzar registrar los datos. El generador de señales comenzará automáticamente.
- 2) En el osciloscopio presione smart cursor
, y muévalo a través de los peak de la curva del voltaje a través de la resistencia, (media traza). Registre el voltaje para el canal B.
- 3) En la ventana Generador de Señales aumente la frecuencia en
- 4) Repita el proceso hasta que alcance los
. A esta frecuencia active el osciloscopio. Ajuste la velocidad de barrido de
a
. Encuentre el valor para
- 5) Active la ventana del Generador de Señales. Aumente la frecuencia a
. Encuentre el nuevo valor de
- 6) Incremente la frecuencia en
y repita el proceso hasta llegar a
.
- 7) A partir de la tabla de datos determine la frecuencia de resonancia (donde el voltaje a través de la resistencia alcanza el valor máximo y el voltaje de salida con el voltaje de la resistencia está, en fase).
- 8) Realice ajustes finos de la frecuencia hasta que la traza del voltaje del canal B esté en fase con la traza de salida.
[edit] Análisis
- 1.- Calcule la corriente que circula a través de la resistencia y registre los valores obtenidos en la tabla de datos.
- 2.- Haga un gráfico Corriente
- 2.- Haga un gráfico Corriente
- 3.- Usando el valor de la frecuencia de resonancia (obtenida del osciloscopio), calcule la frecuencia de resonancia angular y registre el valor en la tabla de datos.
- 4.- Calcule la frecuencia de resonancia angular teórica usando los valores de la inductancia y capacitancia. Compare éste valor con el obtenido en 3.
[edit] Preguntas
- ¿Cuál es el porcentaje de diferencia entre la frecuencia de resonancia angular medida con el valor teórico?.
- ¿Es la curva corriente
- En resonancia, las reactancias del inductor y del capacitor se cancelan las unas a las otras por lo que la impedancia (
) es igual a la resistencia (
). Calcule la resistencia del circuito usando la amplitud de la corriente en resonancia en la ecuación
(donde
es la amplitud del voltaje aplicado) ¿Es ésta resistencia igual a
?.Explique.
