Doblete del Sodio (Fiz0311)

Revision as of 07:22, 23 October 2014

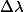$\Delta \lambda$ del Doblete del Sodio (4 completos)

Objetivo

Medir la separación entre las dos líneas amarillas del espectro de Sodio, usando un interferómetro de Michelson.

Equipamiento

-Interferómetro de Michelson

-Lámpara de Sodio

-Lámpara de Mercurio

Introducción

C.Sanchez del Río en una monografía del Consejo Superior de Investigaciones Científicas titulada “Introducción a la Interferometría”, Madrid 1949, afirma: “Las interferencias luminosas han tenido y tienen una doble importancia: por una parte un interés teórico, y por otra, una aplicación técnica. Desde el punto de vista teórico, han representado un papel decisivo en la introducción del concepto de onda en la Ciencia de la Luz. Bajo el aspecto técnico, la aplicación de las interferencias (interferometría), ha permitido el desarrollo de los métodos de la medida más preciso de que dispone hoy, no solo la Optica sino aún, toda la Física.

La interferencia de ondas es el proceso mediante el cual dos o más ondas de la misma naturaleza se combinan para originar una onda cuya amplitud es la suma vectorial de las amplitudes de las ondas que interfieren.

Para observar interferencias con ondas generadas por átomos o moléculas excitadas, es necesario utilizar una fuente única y desdoblar la luz de ésta fuente en partes que puedan recombinarse. En este caso los cambios de amplitud y fase ocurren simultáneamente en cada parte y en el mismo tiempo, o sea, se tiene una situación estacionaria espacio-temporal.

Los interferómetros tienen muchos usos: medidas de longitudes, longitud de onda, de índices de refracción de sólidos, líquidos o gases, etc. La precisión alcanzada en las medidas interferenciales, es altamente apreciada en física e ingeniería.

El interferómetro de que tratamos fue originalmente proyectado por Michelson, para poner de manifiesto el movimiento de la tierra respecto del “éter”.Este experimento lo encontrará Ud. en textos de física moderna a propósito de la teoría de la relatividad de Einstein.

En este experimento su usa el interferómetro de Michelson para medir la separación entre las dos líneas amarillas del doblete del Sodio. El espectro óptico del sodio consiste en algunos pares de líneas llamados dobletes. La separación entre los longitudes de onda de cada línea de un doblete es muy pequeña. Ya que la energía de una línea espectral se determina por la diferencia entre el nivel de energía inicial y final del transición del electrón en el átomo, entonces se insinúa que existen dos niveles de energía iniciales (doblete) con valores muy cercanos en el átomo de sodio. De hecho, las diferencias son demasiado pequeñas para que se pueden explicar solamente de diferencias en el momento angular de las órbitas de los electrones. Como el electrón tiene una propiedad intrinsica llamada ‘spin’, este momento angular “spin” se acopla con el de la órbita y genera dos niveles de energía con distinto momento orbital total ( $J$ ). Este bifurcación de los niveles de energía se llama estructura fina.

Montaje Experimental

Figura 1: Interferómetro de Michelson.

El Interferómetro de Michelson

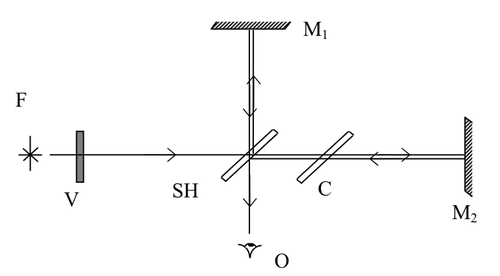
El interferómetro de Michelson (fig.1) es un instrumento que permite estudiar cuantitativamente pequeñas diferencias de espesor, índice de refracción, longitud de onda, etc. Se basa en la interferencia de dos frentes de onda que recorren caminos diferentes. En la Fig. 2 se muestra el montaje experimental básico de un interferómetro de Michelson.

Figura 2: esquema de un interferómetro de Michelson. $F$ , fuente luminosa, $V$ , vidrio esmerilado, $SH$ , separador de haz, $C$ , compensador, $M_1$ y $M_2$ , espejos planos, $O$ , observador.

La luz emitida por la fuente $F$ es difundida por la pantalla de vidrio esmerilado $V$ , y luego separada en dos haces por el separador $SH$ . Los haces viajan hacia los espejos $M_1$ y $M_2$ . La luz es reflejada por los espejos y ambos haces se recombinan en el separador de haces, llegando hasta el observador, $O$ . Ambos haces interfieren, estando las franjas de interferencia determinadas por la posición y orientación de los espejos. El compensador $C$ asegura que los caminos ópticos sean iguales cuando ambos espejos estén a la misma distancia del separador de haces.

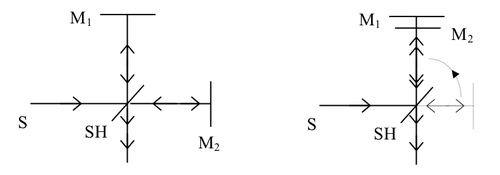
El análisis del instrumento se simplifica al notar que los dos arreglos geométricos siguientes (Fig. 3) son equivalentes.

Figura 3: Arreglos geométricamente equivalentes.

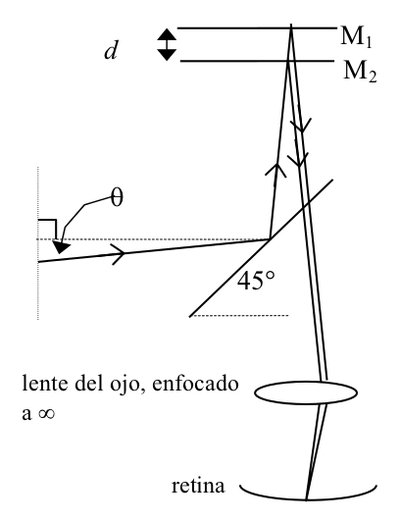
La luz emitida desde la superficie del vidrio esmerilado sale en todas direcciones. Consideremos un rayo particular que es emitido en ángulo $\theta$ respecto del eje horizontal del interferómetro. En el caso en que los espejos están exactamente paralelos, con una separación efectiva $d$ , se tiene el caso que muestra la Fig. 4.

En el caso de los espejos paralelos, la diferencia de camino $\Delta l$ entre los haces reflejados por $M_1$ y $M_2$ es,

$\Delta l= 2d/\cos(\theta) \qquad\qquad\qquad (1)$

donde $d$ es la separación efectiva entre los espejos y $\theta$ es el ángulo en que es emitido el rayo de luz correspondiente. Cuando la diferencia de camino es un múltiplo entero de la longitud de onda, se produce interferencia constructiva, resultando una franja brillante. Esto ocurre para la condición,

$m \lambda= 2d/ \cos(\theta) \qquad\qquad\qquad (2)$

donde $m$ es un entero.

Dada la simetría azimutal en torno al eje del interferómetro, si los espejos están alineados paralelos, el observador percibe las franjas de interferencia como círculos concéntricos, que alternan franjas brillantes y oscuras. De acuerdo con la Ec. (2), el número de franjas, y por lo tanto su espaciamiento, depende del orden $m$ , y del cuociente $\lambda /d$ . El menor número de franjas se produce cuando la separación d es del orden de la longitud de onda $\lambda$ .

Figura 4: Espejos paralelos con formación de franjas circulares.

Montaje Experimental

Alineación de la lámpara

1) Instale la lámpara al costado del interferómetro. Coloque el filtro verde y el vidrio esmerilado en posición correspondiente. Encienda la lámpara de Mercurio. Ponga la flecha metálica sobre el vidrio esmerilado, de modo que se vea claramente en el campo visual. Usted debe poder ver tres imágenes de la flecha. Una de ellas debe ser ignorada (para decidir cual de ellas es ignorable, mire la Fig. 2). Ajuste los tornillos de $M_2$ , hasta que las otras dos imágenes se superpongan. Esto asegura que $M_1$ y $M_2$ estén aproximadamente paralelos.

2) En estas condiciones es posible percibir franjas de interferencia en el campo visual. Si ello no ocurre, haga pequeños ajustes a los tornillos de $M_2$ , hasta lograrlo. Realice a continuación ajustes más finos, hasta ver franjas circulares centradas en el campo visual. En estas condiciones el espectrómetro se encuentra alineado.

Parte I: Observaciones Cualitativas y Calibración del Interferómetro

1. Mueva el tornillo micrométrico que permite desplazar el espejo $M_1$ , produciendo una variación del espaciamiento efectivo $d$ . Observe como las franjas colapsan hacia el centro o surgen desde la parte central, dependiendo de la dirección del desplazamiento. Explique lo que ocurre.

2. Observando las franjas y el puntero, introduzca sin tocar nada, uno de sus dedos en el haz que va desde el semiespejo al espejo fijo. ¿Qué sucede?, ¿Qué ha modificado Ud.?, ¿Cómo lo explica?

3. Observando las franjas y el puntero, trate de golpear la base del interferómetro ¿Qué observa?

Entre el micrómetro y el espejo hay una palanca que reduce el desplazamiento. Así el desplazamiento del espejo, $d$ , no es igual al del micrómetro, $D\mu$ . Hay una reducción constante de un factor $\eta$ , entonces

$d=\eta \cdot D_{\mu} \qquad\qquad\qquad (3)$

El instrumento debe ser calibrado, es decir se debe calcular $\eta$ , usando una línea espectral de longitud de onda conocida. La línea verde del Mecurio corresponde a una longitud de onda de $546.1 nm$ .

4. Mueva ligeramente uno de los tornillos de $M_2$ , hasta que las franjas circulares cambien a cuasi-paralelas. Gire muy lentamente el tornillo micrométrico unas cinco divisiones y cuente el número de franjas de interferencia que pasan frente al puntero indicador. ¿Qué distancia ha avanzado el micrometro? ¿Qué distancia ha avanzado el espejo móvil?, ¿Entonces, cual es el valor de $\eta$ ? ¿Cual es la fuente de error mas grande en este medicion? Tome varios mediciones y obtenga $\eta$ y su error.

Parte II : Mediciones de la Diferencia entre las Longitudes de Onda de dos Líneas muy cercanas

Teoría

Como dice la introducción, la luz emitida por una lámpara de sodio de baja presión consiste en algunas líneas y dobletes. En realidad el doblete amarillo es mucho más brillante que los otros y entonces se puede considerar la luz que sale de la lámpara como cuasi-monocromática, con dos lineas muy cercanas a $589 nm$ .

Con la lámpara de sodio como fuente de luz para el interferómetro, cada línea del doblete, correspondiente a $\lambda_1$ y $\lambda_2$ , produce su propio patrón de interferencia. A la salida del interferómetro se ven los dos patrones superpuestos. De acuerdo con la Ec. (2), por un desplazamiento del espejo $M_1$ el número de franjas que pasan por la flecha será diferente para cada patrón.

Supongamos que para una posición del espejo dos franjas brillantes, una correspondiente a la línea 1 y otra a la línea 2, en el centro del campo visual. En esta posición se ven franjas muy claras, es decir, con una visibilidad o contraste máximo. Mientras se desplaza el espejo los dos patrones que se superponen en el campo visual, quedan mal alineados porque el desplazamiento de las franjas es un poco diferente para $\lambda_1$ y para $\lambda_2$ .

Eventualmente se alcanza un desplazamiento del espejo donde una franja brillante correspondiente a $\lambda_1$ coincide con una franja oscura correspondiente a $\lambda_2$ . En esta posición no se ven franjas claras, es decir, la visibilidad o contraste es mínimo. Con más desplazamiento del espejo se encontrará una posición donde, de nuevo, una franja brillante coincide con otra brillante y la visibilidad es máxima. Entonces al desplazar el espejo $M_1$ se ve una cambio periódico de la visibilidad de las franjas. Por medio del período de este cambio de visibilidad se puede calcular el $\Delta \lambda$ del doblete. Sea $d$ la separación entre los espejos para esta situación. Si hay una franja brillante correspondiente a $\lambda_1$ en el centro del campo visual (donde $\theta = 0$ y $\cos(\theta) = 1$ ), se puede escribir,

$2d=m_1 \lambda_1 \qquad\qquad\qquad (4)$

por lo que,

$\lambda_1=\frac{2d}{m_1} \qquad\qquad\qquad (5)$

Para la condición de mínima visibilidad, debe haber una franja oscura en el patrón de $\lambda_2$ en este punto. De modo que,

$2d=(m_2+1/2)\lambda_2 \qquad\qquad\qquad (6)$

donde,

$\lambda_2=\frac{2d}{(m_2+1/2)} \qquad\qquad\qquad (7)$

Restando, ec.(5) - ec. (7)

$\lambda_1-\lambda_2=2d\frac{(m_2-m_1)+1/2}{m_1(m_2+1/2)} \qquad\qquad\qquad (8)$

Ahora, multiplicando la ec.(5) con la ec.(7),

$\lambda_1\lambda_2=\frac{4d^2}{m_1(m_2+1/2)} \qquad\qquad\qquad (9)$

Haciendo $\lambda_1-\lambda_2=\Delta \lambda$ y $\lambda_1\lambda_2=\lambda^2$ , se tiene,

$d=\frac{\lambda^2}{2\Delta \lambda}(m_2-m_1+1/2) \qquad\qquad\qquad (10)$

Partiendo desde $d = 0$ , la condición de mínima visibilidad ocurre para valores de $d$ correspondientes a $(m2 - m1) = 0, \pm 1, \pm 2$ , etc.

Procedimiento Experimental

Reemplace la lámpara de Mercurio por la lámpara de Sodio, cuidando de no alterar el alineamiento del interferómetro.

Con el micrómetro, mueva el espejo $LaTeX: M_1$ , hasta obtener una condición de mínima visibilidad de las franjas. Anote el valor de $LaTeX: d$ correspondiente.

Desplace $LaTeX: M_1$ registrando los valores sucesivos de $LaTeX: d$ a los cuales se produce nuevamente la condición de mínima visibilidad.

Usando un metodo gráfico y la ec.10 obtenga $LaTeX: \Delta \lambda$ y su error a partir de la pendiente del gráfico. Para esto use el hecho que $LaTeX: |m_2 - m_1|$ cambia en uno para posiciones adyacentes de mínima visibilidad. Use $LaTeX: \lambda = 589 nm$ , para $LaTeX: \lambda_1 \approx \lambda_2$ . Recuerde que debe incluir el error en $LaTeX: \eta$ en su cálculo del error de $LaTeX: \Delta \lambda$ . (¿Porqué?)

Compare con los valores de tabla para $LaTeX: \Delta \lambda$ .

@@ Line 103: / Line 103: @@
 === Teoría ===
-Como dice la introducción, la luz emitida por una lámpara de sodio de baja presión consiste en algunas líneas y dobletes. En realidad el doblete amarillo es mucho más brillante que los otros y entonces se puede considerar la luz que sale de la lámpara como cuasi-monocromática, con dos lineas muy cercanas a <math>589 nm</math>.
+Como dice la introducción, la luz emitida por una lámpara de sodio de baja presión consiste en algunas líneas y dobletes. En realidad el doblete amarillo es mucho más brillante que los otros y entonces se puede considerar la luz que sale de la lámpara como cuasi-monocromática, con dos lineas muy cercanas a <m>589 nm</m>.
-Con la lámpara de sodio como fuente de luz para el interferómetro, cada línea del doblete, correspondiente a <math>\lambda_1</math> y <math>\lambda_2</math>, produce su propio patrón de interferencia. A la salida del interferómetro se ven los dos patrones superpuestos. De acuerdo con la Ec. (2), por un desplazamiento del espejo <math>M_1</math> el número de franjas que pasan por la flecha será diferente para cada patrón.
+Con la lámpara de sodio como fuente de luz para el interferómetro, cada línea del doblete, correspondiente a <m>\lambda_1</m> y <m>\lambda_2</m>, produce su propio patrón de interferencia. A la salida del interferómetro se ven los dos patrones superpuestos. De acuerdo con la Ec. (2), por un desplazamiento del espejo <m>M_1</m> el número de franjas que pasan por la flecha será diferente para cada patrón.
-Supongamos que para una posición del espejo dos franjas brillantes, una correspondiente a la línea 1 y otra a la línea 2, en el centro del campo visual. En esta posición se ven franjas muy claras, es decir, con una visibilidad o contraste máximo. Mientras se desplaza el espejo los dos patrones que se superponen en el campo visual, quedan mal alineados porque el desplazamiento de las franjas es un poco diferente para <math>\lambda_1</math> y para <math>\lambda_2</math>.
+Supongamos que para una posición del espejo dos franjas brillantes, una correspondiente a la línea 1 y otra a la línea 2, en el centro del campo visual. En esta posición se ven franjas muy claras, es decir, con una visibilidad o contraste máximo. Mientras se desplaza el espejo los dos patrones que se superponen en el campo visual, quedan mal alineados porque el desplazamiento de las franjas es un poco diferente para <m>\lambda_1</m> y para <m>\lambda_2</m>.
-Eventualmente se alcanza un desplazamiento del espejo donde una franja brillante correspondiente a <math>\lambda_1</math> coincide con una franja oscura correspondiente a <math>\lambda_2</math>. En esta posición no se ven franjas claras, es decir, la visibilidad o contraste es mínimo. Con más desplazamiento del espejo se encontrará una posición donde, de nuevo, una franja brillante coincide con otra brillante y la visibilidad es máxima. Entonces al desplazar el espejo <math>M_1</math> se ve una cambio periódico de la visibilidad de las franjas. Por medio del período de este cambio de visibilidad se puede calcular el <math>\Delta \lambda</math> del doblete. Sea <math>d</math> la separación entre los espejos para esta situación. Si hay una franja brillante correspondiente a <math>\lambda_1</math> en el centro del campo visual (donde <math>\theta = 0</math> y <math>\cos(\theta) = 1</math>), se puede escribir,
+Eventualmente se alcanza un desplazamiento del espejo donde una franja brillante correspondiente a <m>\lambda_1</m> coincide con una franja oscura correspondiente a <m>\lambda_2</m>. En esta posición no se ven franjas claras, es decir, la visibilidad o contraste es mínimo. Con más desplazamiento del espejo se encontrará una posición donde, de nuevo, una franja brillante coincide con otra brillante y la visibilidad es máxima. Entonces al desplazar el espejo <m>M_1</m> se ve una cambio periódico de la visibilidad de las franjas. Por medio del período de este cambio de visibilidad se puede calcular el <m>\Delta \lambda</m> del doblete. Sea <m>d</m> la separación entre los espejos para esta situación. Si hay una franja brillante correspondiente a <m>\lambda_1</m> en el centro del campo visual (donde <m>\theta = 0</m> y <m>\cos(\theta) = 1</m>), se puede escribir,
-:::<math>2d=m_1 \lambda_1 \qquad\qquad\qquad (4)</math>
+:::<m>2d=m_1 \lambda_1 \qquad\qquad\qquad (4)</m>
 por lo que,
-:::<math>\lambda_1=\frac{2d}{m_1} \qquad\qquad\qquad (5)</math>
+:::<m>\lambda_1=\frac{2d}{m_1} \qquad\qquad\qquad (5)</m>
-Para la condición de mínima visibilidad, debe haber una franja oscura en el patrón de <math>\lambda_2</math> en este punto. De modo que,
+Para la condición de mínima visibilidad, debe haber una franja oscura en el patrón de <m>\lambda_2</m> en este punto. De modo que,
-:::<math>2d=(m_2+1/2)\lambda_2 \qquad\qquad\qquad (6)</math>
+:::<m>2d=(m_2+1/2)\lambda_2 \qquad\qquad\qquad (6)</m>
 donde,
-:::<math>\lambda_2=\frac{2d}{(m_2+1/2)} \qquad\qquad\qquad (7)</math>
+:::<m>\lambda_2=\frac{2d}{(m_2+1/2)} \qquad\qquad\qquad (7)</m>
 Restando, ec.(5) - ec. (7)
-:::<math>\lambda_1-\lambda_2=2d\frac{(m_2-m_1)+1/2}{m_1(m_2+1/2)} \qquad\qquad\qquad (8)</math>
+:::<m>\lambda_1-\lambda_2=2d\frac{(m_2-m_1)+1/2}{m_1(m_2+1/2)} \qquad\qquad\qquad (8)</m>
 Ahora, multiplicando la ec.(5) con la ec.(7),
-:::<math>\lambda_1\lambda_2=\frac{4d^2}{m_1(m_2+1/2)} \qquad\qquad\qquad (9)</math>
+:::<m>\lambda_1\lambda_2=\frac{4d^2}{m_1(m_2+1/2)} \qquad\qquad\qquad (9)</m>
-Haciendo <math>\lambda_1-\lambda_2=\Delta \lambda</math> y <math>\lambda_1\lambda_2=\lambda^2</math>, se tiene,
+Haciendo <m>\lambda_1-\lambda_2=\Delta \lambda</m> y <m>\lambda_1\lambda_2=\lambda^2</m>, se tiene,
-:::<math>d=\frac{\lambda^2}{2\Delta \lambda}(m_2-m_1+1/2) \qquad\qquad\qquad (10)</math>
+:::<m>d=\frac{\lambda^2}{2\Delta \lambda}(m_2-m_1+1/2) \qquad\qquad\qquad (10)</m>
-Partiendo desde <math>d = 0</math>, la condición de mínima visibilidad ocurre para valores de <math>d</math> correspondientes a <math>(m2 - m1) = 0, \pm 1, \pm 2</math>, etc.
+Partiendo desde <m>d = 0</m>, la condición de mínima visibilidad ocurre para valores de <m>d</m> correspondientes a <m>(m2 - m1) = 0, \pm 1, \pm 2</m>, etc.
 == Procedimiento Experimental ==

Doblete del Sodio (Fiz0311)

Revision as of 07:22, 23 October 2014

Contents

$\Delta \lambda$ del Doblete del Sodio (4 completos)

Objetivo

Equipamiento

Introducción

Montaje Experimental

El Interferómetro de Michelson

Montaje Experimental

Parte I: Observaciones Cualitativas y Calibración del Interferómetro

Parte II : Mediciones de la Diferencia entre las Longitudes de Onda de dos Líneas muy cercanas

Teoría

Procedimiento Experimental

Views

Personal tools

Navigation

Search

Tools

Print/export