Interferencia y Difracción (Fiz0312)
(→Extras:) |
(→Introducción) |
||
| Line 16: | Line 16: | ||
El patrón de difracción está dado por: |
El patrón de difracción está dado por: |
||
| − | :<center><math>I(x)=I_0 \frac{1}{2}\left[\left(\frac{1}{2}+C\sqrt{\frac{2}{\lambda z_0}} x\right)^2+\left(\frac{1}{2}+S\sqrt{\frac{2}{\lambda z_0}} x\right)^2\right] \qquad\qquad\qquad (1)</math> </center> |
+ | :<center><m>I(x)=I_0 \frac{1}{2}\left[\left(\frac{1}{2}+C\sqrt{\frac{2}{\lambda z_0}} x\right)^2+\left(\frac{1}{2}+S\sqrt{\frac{2}{\lambda z_0}} x\right)^2\right] \qquad\qquad\qquad (1)</m> </center> |
| − | Donde <math>I_0 </math> es la intensidad de la luz en el plano z=0, y donde C y S son las "integrales de Fresnel": |
+ | Donde <m>I_0 </m> es la intensidad de la luz en el plano z=0, y donde C y S son las "integrales de Fresnel": |
| − | :<center><math>C(x)=\int_0^x \! cos(\frac{\pi}{2} t^2) \, \mathrm{d}t. \qquad\qquad\qquad </math> </center> |
+ | :<center><m>C(x)=\int_0^x \! cos(\frac{\pi}{2} t^2) \, \mathrm{d}t. \qquad\qquad\qquad </m> </center> |
| − | :<center><math>S(x)=\int_0^x \! sin(\frac{\pi}{2} t^2) \, \mathrm{d}t. \qquad\qquad\qquad </math> </center> |
+ | :<center><m>S(x)=\int_0^x \! sin(\frac{\pi}{2} t^2) \, \mathrm{d}t. \qquad\qquad\qquad </m> </center> |
===Equipamiento=== |
===Equipamiento=== |
||
Revision as of 14:29, 22 October 2014
Contents |
Interferencia y Difracción
Objetivo
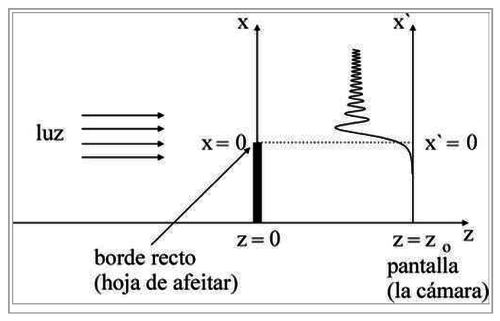
Estudiar el patrón de difracción por un borde recto.
Introducción
Al iluminar un borde recto con un haz de luz monocromático y un frente de onda plano se produce un patrón de difracción en una pantalla.
El patrón de difracción está dado por:
Donde es la intensidad de la luz en el plano z=0, y donde C y S son las "integrales de Fresnel":
Equipamiento
- Láser ().
- hoja de afeitar con soporte
- una cámara
- software para ver y analizar imágenes (ImageJ 1.46)
Procedimiento Experimental
Montaje Básico
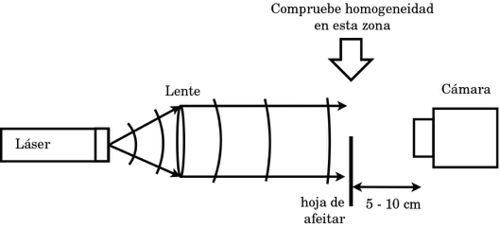
1. Por difracción, el frente de onda generado por el láser no es plano ni homogéneo. Por lo tanto, es necesario remover el pequeño lente que viene con el láser y lograr que el haz sea colimado con un lente externo.
2. La distancia entre la hoja de afeitar y el láser debe ser suficientemente grande para que la onda que llega a esta tenga un frente plano y una intensidad homogénea. Para esto, coloque la hoja de afeitar a una distancia prudente de su láser.
3. Para verificar que la intensidad cerca de la hoja de afeitar sea homogénea utilice la cámara. Para ello compruebe que la imagen de la luz en la posición donde se pondrá la hoja de afeitar sea lo más homogénea posible, para luego poner dicha hoja en ese lugar.
4. Para medir el patrón de difracción, la distancia entre la hoja de afeitar y la cámara debería ser aproximadamente entre 5 cm y 10 cm.
Medición:
1. Obtenga mediciones de la distribución de intensidades para al menos tres valores de la distancia z0. Se tiene que obtener un patrón como se muestra en la figura.
2. Como se ve en la figura las líneas de difracción deben ser verticales. En caso de que existan manchas, hay que limpiar el chip de la cámara con papel apropiado y alcohol.
Análisis de básico de datos:
1. Utilice el software ImageJ 1.46 para hacer cortes transversales de la imagen y grafíquelas (para ello use las opciones que nos da el programa en la opción "Analize").
2. A partir de estos resultados y conociendo la distancia z0 ajuste una curva para obtener la longitud de onda del láser. Utilice las aproximaciones, válidas para x>2, dadas por:
3. Compare la longitud de onda obtenida con la información que tienen ustedes sobre el láser.
Partes Adicionales:
Usando materiales asociados a los montajes previos, y algunos recursos extra disponibles en el laboratorio, usted podría estudiar:
- Difracción por una rendija. Con una rendija de lineas/mm conocida, corrobore la longitud de onda de su láser. También puede ser el camino inverso. Es decir, asumiendo conocida la longitud de onda del láser, calcule las lineas/mm de su rendija
- Difracción por un CD. Determine cuántas lineas/mm tiene un CD.
- Difracción por patrones de figuras (círculo, cuadrado, etc.). Analice patrones de figuras conocidas, y compare con la teoría. Por ejemplo, para una apertura circular, vea el disco de Airy.
En esta sección, usted debe elegir al menos uno de estos fenómenos para estudiar. Debe registrar en su Acta lo que está analizando, cómo lo hace, los inconvenientes y resultados obtenidos, análisis, etc. Si usted se le ocurre algo interesante de medir, dentro del contexto del curso, puede agregarlo a la lista de “Adicionales”